题目内容
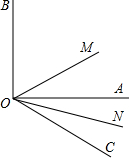 如图,∠AOB是直角,∠AOC=30°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的度数.
如图,∠AOB是直角,∠AOC=30°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的度数.考点:角的计算,角平分线的定义
专题:
分析:求出∠BOC,根据角平分线定义求出∠NOC和∠MOC,相减即可求出答案.
解答:解:∵∠AOB是直角,∠AOC=30°,
∴∠BOC=120°,
∵ON是∠AOC的平分线,OM是∠BOC的平分线,
∴∠NOC=
∠AOC=15°,∠MOC=
∠BCO=60°,
∴∠MON=∠MOC-∠NOC=60°-15°=45°.
∴∠BOC=120°,
∵ON是∠AOC的平分线,OM是∠BOC的平分线,
∴∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠MOC-∠NOC=60°-15°=45°.
点评:本题考查了角平分线定义,角的有关计算的应用,解此题的关键是求出∠NOC和∠MOC的大小.

练习册系列答案
相关题目
下列条件中,不能判断ABC为直角三角形的是( )
| A、a=3,b=4,c=5 |
| B、∠A+∠B=∠C |
| C、a=1,b=2,c=3 |
| D、∠A:∠B:∠C=1:2:3 |

 如图,四边形ABCD中,E是AD中点,CE交BA延长线于点F.此时E也是CF中点
如图,四边形ABCD中,E是AD中点,CE交BA延长线于点F.此时E也是CF中点 如图,四边形ABCD是直角梯形,AD∥BC,∠B=90°,AB=8cm,AD=24cm.BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动.设运动的时间为t(秒).
如图,四边形ABCD是直角梯形,AD∥BC,∠B=90°,AB=8cm,AD=24cm.BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动.设运动的时间为t(秒). 夏天到了,欣欣服装店老板用4500元购进一批卡通团T桖衫,由于深受顾客喜爱,很快售完,老板又用5000元购进第二批该款式T恤杉,所购数量与第一批相同,但每件进价比第一批多了10元.
夏天到了,欣欣服装店老板用4500元购进一批卡通团T桖衫,由于深受顾客喜爱,很快售完,老板又用5000元购进第二批该款式T恤杉,所购数量与第一批相同,但每件进价比第一批多了10元.