题目内容
3. 人民公园划出一块矩形区域,用以栽植鲜花.
人民公园划出一块矩形区域,用以栽植鲜花.(1)经测量,该矩形区域的周长是72m,面积为320m2,请求出该区域的长与宽;
(2)公园管理处曾设想使矩形的周长和面积分别为(1)中区域的周长和面积的一半,你认为此设想合理吗?如果此设想合理,请求出其长和宽;如果不合理,请说明理由,并求出在(1)中周长减半的条件下矩形面积的最大值.
分析 (1)设矩形的一边长为x,则另一边的长为36-x米,利用矩形的面积计算方法列出方程求解即可;
(2)设矩形的一边长为y,根据题意得矩形的另一边的长为(18-y)米,利用矩形的面积计算方法列出方程后用根的判别式进行判断即可.
解答 解:(1)设矩形的一边长为x,则另一边的长为36-x米,根据题意得:
x(36-x)=320,
解得:x=20或x=16,
答:矩形的长和宽分别为20米和16米;
(2)设矩形的一边长为y,根据题意得矩形的另一边的长为(18-y)米,
根据题意得:y(18-y)=160,
整理得:y2-18y+160=0,
∵△=b2-4ac=(-18)2-4×160=-316<0,
∴此设想不合理.
设周长减少一半后的一边的长为y,则另一边的长为18-y米,
面积S=y(18-y)=-y2+18y=-(y-9)2+81,
所以面积的最大值为81平方米.
点评 本题考查了一元二次方程的应用,解题的关键是根据题意表示出矩形的长和宽,从而根据矩形的面积的计算方法列出方程求解.

练习册系列答案
相关题目
13.已知 am+2n•bn+2•(bm)2=a5b6,则m+n的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18. 如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )
如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )
 如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )
如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )| A. | 矩形 | B. | 菱形 | C. | 矩形或菱形 | D. | 正方形 |
 如图,在△ABC中,∠C=90°,M为斜边AB上的一点,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:3,求AN的长.
如图,在△ABC中,∠C=90°,M为斜边AB上的一点,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:3,求AN的长. 某路基的横截面如图所示,路基高BC=1m,斜坡AB的坡度为1:2,则斜坡AB的长为$\sqrt{5}$m.
某路基的横截面如图所示,路基高BC=1m,斜坡AB的坡度为1:2,则斜坡AB的长为$\sqrt{5}$m. 如图,已知AB∥ED,∠B=120°,∠D=140°.求∠BCD的度数.
如图,已知AB∥ED,∠B=120°,∠D=140°.求∠BCD的度数. 如图,TQ切⊙O于点A,∠BAQ=60°,连接BO并延长与⊙O交于点C,与OA的延长线交于点T,若TC=2,求TA的长.
如图,TQ切⊙O于点A,∠BAQ=60°,连接BO并延长与⊙O交于点C,与OA的延长线交于点T,若TC=2,求TA的长.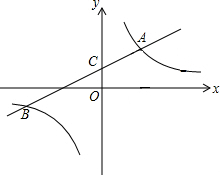 如图,一次函数y1=k1x+1与反比例函数y2=$\frac{k_2}{x}$的图象交于点A(3,2)和点B,与y轴交于点C.
如图,一次函数y1=k1x+1与反比例函数y2=$\frac{k_2}{x}$的图象交于点A(3,2)和点B,与y轴交于点C. 如图,已知AB=AE,∠1+∠2=∠3,∠ABC=∠AED=90°,求证:BC+DE=CD.
如图,已知AB=AE,∠1+∠2=∠3,∠ABC=∠AED=90°,求证:BC+DE=CD.