��Ŀ����
18����ͼ1�����ı���ABCD�У���D=60�㣬��P��Qͬʱ�ӵ�D��������ÿ��1����λ���ȵ��ٶȷֱ���D��A��B��C��D��C��B�����˶�������ʱֹͣ������PQ�����P�˶���·��Ϊx��PQ�ij�y��y��x֮������ĺ�����ϵ��ͼ����ͼ2��������˵���в���ȷ���ǣ�������
| A�� | AB��CD | B�� | AB=8 | ||
| C�� | S�ı���ABCD=$\frac{161\sqrt{3}}{4}$ | D�� | ��B=135�� |
���� ��ͼ���֪�ı���ABCD�ǵ������Σ�����AD=BC=7��AB=8��BC=15���ɽ�����⣮
��� �⣺��ͼ���֪���ı���ABCD�ǵ������Σ�
��AD=BC=7��AB=8��BC=15��
��AB��CD����A��B��ȷ��
��S����ABCD=$\frac{8+15}{2}•\frac{\sqrt{3}}{2}•7$=$\frac{161\sqrt{3}}{4}$����C��ȷ��
�ߡ�A+��D=180�㣬��D=60�㣬
���B=��A=120���D����
��ѡD��
���� ���⿼��ƽ��ֱ������ϵ���й�֪ʶ���������ε��й�֪ʶ����ȷ����ͼ����Ϣ�ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
18�� ��ͼ��ƽ���ı��Ρ����Ρ����Ρ������εİ�����ϵ������ͼ��ʾ����ͼ����Ӱ��������ʾ��ͼ���ǣ�������
��ͼ��ƽ���ı��Ρ����Ρ����Ρ������εİ�����ϵ������ͼ��ʾ����ͼ����Ӱ��������ʾ��ͼ���ǣ�������
 ��ͼ��ƽ���ı��Ρ����Ρ����Ρ������εİ�����ϵ������ͼ��ʾ����ͼ����Ӱ��������ʾ��ͼ���ǣ�������
��ͼ��ƽ���ı��Ρ����Ρ����Ρ������εİ�����ϵ������ͼ��ʾ����ͼ����Ӱ��������ʾ��ͼ���ǣ�������| A�� | ���� | B�� | ���� | C�� | ���λ����� | D�� | ������ |
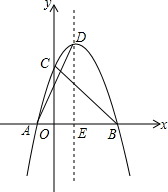 ������y=ax2+bx+3������A��-2��0����B��4��0������y�ύ�ڵ�C��
������y=ax2+bx+3������A��-2��0����B��4��0������y�ύ�ڵ�C��
 ��ͼ����֪AB=AE����1+��2=��3����ABC=��AED=90�㣬��֤��BC+DE=CD��
��ͼ����֪AB=AE����1+��2=��3����ABC=��AED=90�㣬��֤��BC+DE=CD�� ��ͼ���ڡ�ABC�У���D��E��F�ֱ���BC��AB��AC�ϣ�BD=CF��BE=CD��DG��EF�ڵ�G����EG=FG����֤��AB=AC��
��ͼ���ڡ�ABC�У���D��E��F�ֱ���BC��AB��AC�ϣ�BD=CF��BE=CD��DG��EF�ڵ�G����EG=FG����֤��AB=AC�� ��֪��ABCΪ�ȱ������Σ��ӳ�BC��M��CA��N��ʹCM=AN����BN��MA���ӳ�����Q�����BQM��
��֪��ABCΪ�ȱ������Σ��ӳ�BC��M��CA��N��ʹCM=AN����BN��MA���ӳ�����Q�����BQM��