题目内容
5.函数y=$\sqrt{x}$中的自变量x的取值范围是( )| A. | x≥0 | B. | x≤0 | C. | x>0 | D. | x=0 |
分析 根据二次根式的性质:被开方数大于等于0,即可求解.
解答 解:依题意,得x≥0,
故选A.
点评 本题考查的是函数自变量取值范围的求法.函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数为非负数.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
15. 现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
 现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )| A. | 0.8πcm2 | B. | 3.2πcm2 | C. | 4πcm2 | D. | 4.8πcm2 |
20.已知点A(4,3),AB∥y轴,且AB=3,则B点的坐标为( )
| A. | (7,3) | B. | (7,3)或(7,3) | C. | (4,6) | D. | (4,6)或(4,0) |
10.对于一次函数y=-2x+4,下列结论错误的是( )
| A. | 函数值随自变量的增大而减小 | |
| B. | 当x<0时,y<4 | |
| C. | 函数的图象向下平移4个单位长度得y=-2x的图象 | |
| D. | 函数的图象与y轴的交点坐标是(0,4) |
17. 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )| A. | 8+6$\sqrt{3}$ | B. | 12$\sqrt{3}$ | C. | 19.2 | D. | 20 |
 如图,若A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,若A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.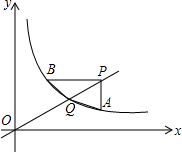 如图,直线y=mx与反比例函数y=$\frac{k}{x}$(x>0)的图象交于Q点,点A,点B都在反比例函数y=$\frac{k}{x}$的图象上,点P在OQ延长线上,且PA∥y轴,PB∥x轴,且连结AQ,BQ,已知B(3,4).
如图,直线y=mx与反比例函数y=$\frac{k}{x}$(x>0)的图象交于Q点,点A,点B都在反比例函数y=$\frac{k}{x}$的图象上,点P在OQ延长线上,且PA∥y轴,PB∥x轴,且连结AQ,BQ,已知B(3,4).