题目内容
10.对于一次函数y=-2x+4,下列结论错误的是( )| A. | 函数值随自变量的增大而减小 | |
| B. | 当x<0时,y<4 | |
| C. | 函数的图象向下平移4个单位长度得y=-2x的图象 | |
| D. | 函数的图象与y轴的交点坐标是(0,4) |
分析 由一次项系数k=-2<0即可得出该函数为减函数,由此得出A正确;将x=0代入函数解析式中求出y值,结合函数的单调性即可得知B不正确;根据图象平移的规律“上加下减”,在函数解析式后面-4整理后即可得知C正确;将x=0代入函数解析式中求出y值,即可得知D正确.此题得解.
解答 解:A、在y=-2x+4中k=-2<0,
∴y随x的增大而减小,即A正确;
B、令y=-2x+4中x=0,则y=4,
∴当x<0时,y>4,即B不正确;
C、函数的图象向下平移4个单位长度后得到的图象的解析式为y=-2x+4-4=-2x,
∴C正确;
D、令y=-2x+4中x=0,则y=4,
∴函数的图象与y轴的交点坐标是(0,4),即D正确.
故选B.
点评 本题考查了一次函数的性质、一次函数图象上点的坐标特点以及图象平移的性质,解题的关键是逐条分析四条选项.本题属于基础题,难度不大,解决该题时,熟悉一次函数的性质、一次函数图象上点的坐标特征以及图象平移的性质是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
5.函数y=$\sqrt{x}$中的自变量x的取值范围是( )
| A. | x≥0 | B. | x≤0 | C. | x>0 | D. | x=0 |
15.下面四个几何体中,主视图是三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.抛物线y=-3x2+2x-l的图象与坐标轴交点的个数是( )
| A. | 没有交点 | B. | 只有一个交点 | C. | 两个交点 | D. | 三个交点 |
19.在Rt△ABC中,∠B=90°,∠C=30°,AC=2,则AB的长为( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
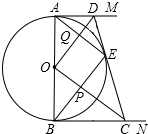 如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:
如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:
 如图是由5个相同的小立方块组成的立体图形,则它的俯视图是( )
如图是由5个相同的小立方块组成的立体图形,则它的俯视图是( )


