题目内容
19.从2开始,连续的偶数相加,它们和的情况如下表:| 加数的个数n | 和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=n(n+1).
(3)根据上题的规律求102+104+106+108+…+200的值(要有过程)
分析 (1)根据表中的规律发现:若n=8时,则S的值为8×9,求得数值即可;
(2)根据表中的规律发现:第n个式子的和是n(n+1);
(3)首先确定有几个加数,由上述可得规律:加数的个数为最后一个加数÷2,据此解答.
解答 解:(1)当n=8时,S=8×9=72;
故答案为:72;
(2)根据特殊的式子即可发现规律,S=2+4+6+8+…+2n=2(1+2+3+…+n)=n(n+1);
故答案为:n(n+1);
(3)102+104+106+…+200
=(2+4+6+…+102+…+200)-(2+4+6+…+100)
=100×101-50×51
=7550.
点评 本题主要考查了规律型问题:数字的变化,解题时注意根据所给的具体式子观察结果和数据的个数之间的关系.认真观察、仔细思考,善用联想是解决这类问题的方法.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 如图,已知动点A在函数y=$\frac{4}{x}$(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴、y轴于点P、Q,当QE:DP=1:4时,图中的阴影部分的面积等于5.
如图,已知动点A在函数y=$\frac{4}{x}$(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴、y轴于点P、Q,当QE:DP=1:4时,图中的阴影部分的面积等于5.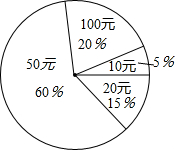 在雅安地震救灾捐款活动中,某校6000名同学每人都捐了款,有捐10元的,有捐20元的,还有捐50元、100元的,如图统计图反映了不同捐款的人数和比例,那么该校同学平均每人捐款53.5元.
在雅安地震救灾捐款活动中,某校6000名同学每人都捐了款,有捐10元的,有捐20元的,还有捐50元、100元的,如图统计图反映了不同捐款的人数和比例,那么该校同学平均每人捐款53.5元. 如图,在边长为1的正方形中,被4段$\frac{1}{4}$圆弧所围的阴影部分面积为1-$\sqrt{3}$+$\frac{π}{3}$.
如图,在边长为1的正方形中,被4段$\frac{1}{4}$圆弧所围的阴影部分面积为1-$\sqrt{3}$+$\frac{π}{3}$.