题目内容
19.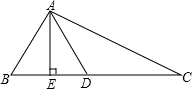 如图,已知AE⊥BC于E,BE=ED,∠BAC=90°,则下列结论不正确的是.
如图,已知AE⊥BC于E,BE=ED,∠BAC=90°,则下列结论不正确的是.| A. | △ABE≌△ADE | B. | ∠ADB与∠C互余 | C. | AD平分∠EAC | D. | AD+AC>BC |
分析 根据全等三角形的判定得出△ABE≌△ADE,再利用全等三角形的性质对各项进行判断即可.
解答 解:在△ABE与△ADE中
$\left\{\begin{array}{l}{BE=ED}\\{∠AEB=∠AED=90°}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△ADE(SAS),故A正确;
∴∠ADB=∠B,
∴∠ADB+∠C=90°,故B正确;
∴AB=AD,
∴AC+AB=AC+AD>BC,故D正确;
但不能得出∠BAD=∠DAC,故C错误;
故选C
点评 此题考查全等三角形的判定和性质,关键是根据全等三角形的判定得出△ABE≌△ADE.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
4.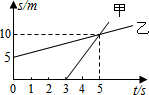 甲、乙两物体沿同一条直线向东运动,其运动的路程S随时间t变化的图象如图所示,以下说法中正确的是( )
甲、乙两物体沿同一条直线向东运动,其运动的路程S随时间t变化的图象如图所示,以下说法中正确的是( )
 甲、乙两物体沿同一条直线向东运动,其运动的路程S随时间t变化的图象如图所示,以下说法中正确的是( )
甲、乙两物体沿同一条直线向东运动,其运动的路程S随时间t变化的图象如图所示,以下说法中正确的是( )| A. | 甲物体比乙物体早运动3s | |
| B. | 甲物体比乙物体运动得慢 | |
| C. | 从第3s开始,v甲>v乙,5s末甲、乙相遇 | |
| D. | 5s内甲、乙两物体的平均速度相等 |
11.已知点C在线段AB的延长线上,5CB=2AC,则$\frac{AC}{AB}$的值是( )
| A. | $\frac{7}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{2}$ | D. | $\frac{5}{2}$ |
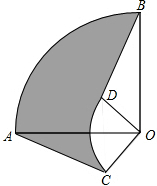 如图,圆心角都是90°的扇形AOB与扇形COD如图叠放在一起,连结AC、BD,若OA=3cm,OC=1cm,则阴影部分的面积为2π平方厘米.
如图,圆心角都是90°的扇形AOB与扇形COD如图叠放在一起,连结AC、BD,若OA=3cm,OC=1cm,则阴影部分的面积为2π平方厘米.
 如图,在△ABC中,AB=AC,DE是腰AB上的中垂线,若∠A=30°,求∠EBC的大小.
如图,在△ABC中,AB=AC,DE是腰AB上的中垂线,若∠A=30°,求∠EBC的大小.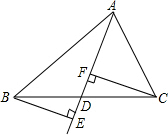 如图,由△ABC的顶点A引一条射线AD,与边BC交于D点,作BE⊥AD于点E,CF⊥AD于点F,为了使BE=CF,射线AD应该具有什么性质?
如图,由△ABC的顶点A引一条射线AD,与边BC交于D点,作BE⊥AD于点E,CF⊥AD于点F,为了使BE=CF,射线AD应该具有什么性质?