题目内容
10.如图,四边形ABCD,EFGH,NHMC都是正方形,边长分别为2,3,m,A,B,N,E,F五点在同一直线上,则正方形CNHM的边长m是多少?
分析 由三个正方形如图的摆放,易证△CBN≌△NEH,从而可在Rt△CBN中利用勾股定理求出CN,即得出c的值.
解答 解:∵四边形ABCD、EFGH、NHMC都是正方形,
∴∠CNB+∠ENH=90°,
又∵∠ENH+∠NHE=90°,
∴∠CNB=∠EHN,
在△CBN和△NEH中,
$\left\{\begin{array}{l}{∠CBN=∠NEH}\\{∠CNB=∠NHE}\\{CN=NH}\end{array}\right.$
∴△CBN≌△NEH,
∴HE=BN=b,
故在Rt△CBN中,BC2+BN2=CN2,
又∵a=2,b=3,
∴m=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$.
则正方形CNHM的边长m是$\sqrt{13}$.
点评 此题考查了勾股定理及三角形全等的判定,解答本题的关键是证明CBN≌△NEH,另外要求我们熟练掌握勾股定理的应用.

练习册系列答案
相关题目
5.某校举办了《为失学儿童募捐活动》,共捐善款12.56万元.将12.56万元用科学记数法表示为( )
| A. | 12.56×104元 | B. | 1.256×105元 | C. | 1.256×104元 | D. | 1256×106元 |
19.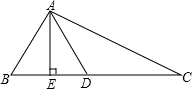 如图,已知AE⊥BC于E,BE=ED,∠BAC=90°,则下列结论不正确的是.
如图,已知AE⊥BC于E,BE=ED,∠BAC=90°,则下列结论不正确的是.
 如图,已知AE⊥BC于E,BE=ED,∠BAC=90°,则下列结论不正确的是.
如图,已知AE⊥BC于E,BE=ED,∠BAC=90°,则下列结论不正确的是.| A. | △ABE≌△ADE | B. | ∠ADB与∠C互余 | C. | AD平分∠EAC | D. | AD+AC>BC |
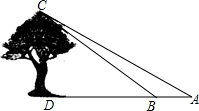 大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71)
大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71)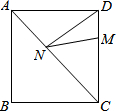 正方形ABCD的边长为12,M在DC上,DM=3,N是AC上的一动点,则DN+MN的最小值是15.
正方形ABCD的边长为12,M在DC上,DM=3,N是AC上的一动点,则DN+MN的最小值是15.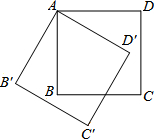 如图,将边长为2cm的正方形ABCD绕点A顺时针旋转到AB′C′D′的位置,∠B′AD=120°,则C点运动到C′点的路径长为$\frac{\sqrt{2}}{3}$πcm.
如图,将边长为2cm的正方形ABCD绕点A顺时针旋转到AB′C′D′的位置,∠B′AD=120°,则C点运动到C′点的路径长为$\frac{\sqrt{2}}{3}$πcm. 在△ABC中,总有$\frac{AB}{sinC}$=$\frac{AC}{sinB}$=$\frac{BC}{sinA}$,利用这个知识请解答下题:
在△ABC中,总有$\frac{AB}{sinC}$=$\frac{AC}{sinB}$=$\frac{BC}{sinA}$,利用这个知识请解答下题: 读图回答问题:
读图回答问题: