题目内容
9.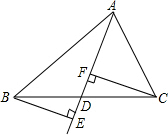 如图,由△ABC的顶点A引一条射线AD,与边BC交于D点,作BE⊥AD于点E,CF⊥AD于点F,为了使BE=CF,射线AD应该具有什么性质?
如图,由△ABC的顶点A引一条射线AD,与边BC交于D点,作BE⊥AD于点E,CF⊥AD于点F,为了使BE=CF,射线AD应该具有什么性质?
分析 当射线AD是BC的中线时,BE=CF,可通过证明△BED≌△CFD证明.
解答 解:当射线AD是BC的中线时,BE=CF,
理由如下:
∵BE⊥AD,CF⊥AD,垂足分别为E,F,
∴∠BED=∠CFD=90°,
∵D是BC中点,
∴BD=CD,
∵∠BDE=∠CFD,
在△BED和△CFD中
$\left\{\begin{array}{l}{∠BED=∠CFD}\\{∠BDE=∠CDF}\\{BD=CD}\end{array}\right.$,
∴△BED≌△CFD(AAS),
∴BE=CF.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BED≌△CFD是解题的关键.

练习册系列答案
相关题目
19.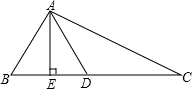 如图,已知AE⊥BC于E,BE=ED,∠BAC=90°,则下列结论不正确的是.
如图,已知AE⊥BC于E,BE=ED,∠BAC=90°,则下列结论不正确的是.
 如图,已知AE⊥BC于E,BE=ED,∠BAC=90°,则下列结论不正确的是.
如图,已知AE⊥BC于E,BE=ED,∠BAC=90°,则下列结论不正确的是.| A. | △ABE≌△ADE | B. | ∠ADB与∠C互余 | C. | AD平分∠EAC | D. | AD+AC>BC |
4. 如图,直角△ABC的周长为24,且AB:AC=5:4,则AC=( )
如图,直角△ABC的周长为24,且AB:AC=5:4,则AC=( )
 如图,直角△ABC的周长为24,且AB:AC=5:4,则AC=( )
如图,直角△ABC的周长为24,且AB:AC=5:4,则AC=( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
 读图回答问题:
读图回答问题: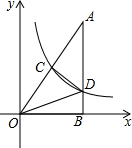 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=18,则S△OBD的值为12.
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=18,则S△OBD的值为12. 如图,已知△ABC≌△BAD,AD与BC交于点E,试说明△ABE是等腰三角形.
如图,已知△ABC≌△BAD,AD与BC交于点E,试说明△ABE是等腰三角形.