��Ŀ����
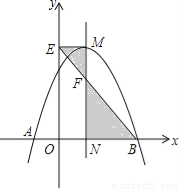
��ͼ�������� ��x�ύ��A��B���㣬���ǵĶԳ�����x�ύ�ڵ�N��������M��ME��y���ڵ�E������BE��MN�ڵ�F.��֪��A������Ϊ����1��0��.
��x�ύ��A��B���㣬���ǵĶԳ�����x�ύ�ڵ�N��������M��ME��y���ڵ�E������BE��MN�ڵ�F.��֪��A������Ϊ����1��0��.
��1����������ߵĽ���ʽ������M�����ꣻ
��2�����EMF���BNF�����֮��.
 ��1������1��4������2��.
�������������������1��ֱ�ӽ�����1��0������������ɣ��������䷽�������������.
��2������EM��BN�����EMF�ס�BNF�����������EMF���BNE�����֮�ȣ�
�����������������
��1���ߵ�A���������ϣ�
�࣬��ã�c=3��
�������ߵĽ���ʽΪ.
�ߣ�
�������ߵĶ���M��1��4����
��2����A����1��0��������...
��1������1��4������2��.
�������������������1��ֱ�ӽ�����1��0������������ɣ��������䷽�������������.
��2������EM��BN�����EMF�ס�BNF�����������EMF���BNE�����֮�ȣ�
�����������������
��1���ߵ�A���������ϣ�
�࣬��ã�c=3��
�������ߵĽ���ʽΪ.
�ߣ�
�������ߵĶ���M��1��4����
��2����A����1��0��������...
ͼ�е�Բ�����й��ɵش��ﵽ��������еģ���yΪ��n�㣨nΪ��������Բ��ĸ����������к�����ϵ����ȷ���ǣ�������
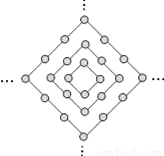
A. y=4n��4 B. y=4n C. y=4n+4 D. y=n2
 B
���������������������ͼ��֪��
n=1ʱ��Բ����4������y=4��
n=2ʱ��Բ����8������y=8��
n=3ʱ��Բ����12������y=12��
����
��y=4n.
��ѡ��B.
B
���������������������ͼ��֪��
n=1ʱ��Բ����4������y=4��
n=2ʱ��Բ����8������y=8��
n=3ʱ��Բ����12������y=12��
����
��y=4n.
��ѡ��B. �۲�������962��95+962��5�Ľ�����̣�������ķ�����( )
A. 962��95+962��5��962��(95+5)��962��100��96200
B. 962��95+962��5��962��5��(19+1)��962��(5��20) ��96200
C. 962��95+962��5��5��(962��19+962)��5��(18278+962)��96200
D. 962��95+962��5��91390+4810��96200
 A
������������962��95+962��5��ֵ����ķ�������ȡ����ʽ962����962��95+962��5��962��(95+5)��962��100��96200����ѡA.
A
������������962��95+962��5��ֵ����ķ�������ȡ����ʽ962����962��95+962��5��962��(95+5)��962��100��96200����ѡA. ����A��2��  ����B��-3��
����B��-3�� 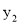 ����C��-1��
����C��-1�� 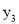 ��������������
��������������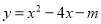 ��ͼ���ϣ���
��ͼ���ϣ��� ��
��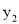 ��
��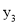 �Ĵ�С��ϵ�ǣ�������
�Ĵ�С��ϵ�ǣ�������
A. 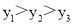
B. 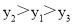
C. 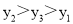
D. 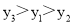
 C
������������������κ�����ͼ��ĶԳ���x==2������a=1��0����֪�俪�����ϣ�Ȼ����A��2�� ����x=2��֪��С������B��-3�� ����C��-1�� �����ڶԳ������࣬���ڶԳ������࣬y��x���������С�����ԣ��ܽ�ɵã�
��ѡ��C��
C
������������������κ�����ͼ��ĶԳ���x==2������a=1��0����֪�俪�����ϣ�Ȼ����A��2�� ����x=2��֪��С������B��-3�� ����C��-1�� �����ڶԳ������࣬���ڶԳ������࣬y��x���������С�����ԣ��ܽ�ɵã�
��ѡ��C�� ��ͼ�Ƕ��κ���y=ax2+bx+c��ͼ�����н��ۣ� �ٶ�������ʽax2+bx+c�����ֵΪ4��
��4a+2b+c��0��
��һԪ���η���ax2+bx+c=1������֮��Ϊ��1��
��ʹy��3������x��ȡֵ��Χ��x��0��
������ȷ�ĸ����У� ��
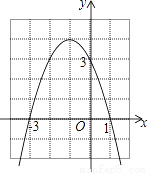
A. 1�� B. 2�� C. 3�� D. 4��
 B
������������������������ߵĶ�������Ϊ��-1��4�������������ʽax2+bx+c�����ֵΪ4������ȷ��
��x=2ʱ��y��0����4a+2b+c��0������ȷ��
���������ߵĶԳ��Կ�֪��һԪ���η���ax2+bx+c=1������֮��Ϊ-2���۴���
ʹy��3������x��ȡֵ��Χ��x��0��x��-2���ܴ���
��ѡB��
B
������������������������ߵĶ�������Ϊ��-1��4�������������ʽax2+bx+c�����ֵΪ4������ȷ��
��x=2ʱ��y��0����4a+2b+c��0������ȷ��
���������ߵĶԳ��Կ�֪��һԪ���η���ax2+bx+c=1������֮��Ϊ-2���۴���
ʹy��3������x��ȡֵ��Χ��x��0��x��-2���ܴ���
��ѡB�� �����κ���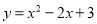 ��Ϊ
��Ϊ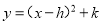 ����ʽ�����Ϊ��������
����ʽ�����Ϊ��������
A. 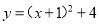
B. 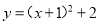
C. 
D. 
 D
��������
��ѡ��D��
D
��������
��ѡ��D�� �������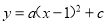 �뺯��
�뺯��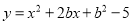 �Ķ�����ͬ��������һ�����������㣨2��7�����������������Ľ���ʽ��
�Ķ�����ͬ��������һ�����������㣨2��7�����������������Ľ���ʽ��
 ��
������������������������뺯���Ķ��㣬Ȼ������������b��c��ֵ��������֪����������һ�����������㣨2��7���������ô���ϵ������ú����Ľ���ʽ��
����������ߺ����Ķ����ǣ�1��c����
�����Ķ����ǣ�-b��-5����
��1=-b����b=-1��c=-5��
�ຯ���Ľ���ʽΪ�� ��
�֡�����һ�����������㣨2��7����
�ຯ�������㣨2��7����
�࣬��ã�a...
��
������������������������뺯���Ķ��㣬Ȼ������������b��c��ֵ��������֪����������һ�����������㣨2��7���������ô���ϵ������ú����Ľ���ʽ��
����������ߺ����Ķ����ǣ�1��c����
�����Ķ����ǣ�-b��-5����
��1=-b����b=-1��c=-5��
�ຯ���Ľ���ʽΪ�� ��
�֡�����һ�����������㣨2��7����
�ຯ�������㣨2��7����
�࣬��ã�a... �����κ���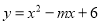 �䷽��Ϊ
�䷽��Ϊ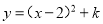 ����m��k��ֵ�ֱ�Ϊ�� ��
����m��k��ֵ�ֱ�Ϊ�� ��
A. 0��6
B. 0��2
C. 4��6
D. 4��2
 D
���������ߣ�
��
�࣬
��-4=-m��4+k=6��
��m=4��k=2��
��ѡ��D��
D
���������ߣ�
��
�࣬
��-4=-m��4+k=6��
��m=4��k=2��
��ѡ��D�� ����2��x��1ʱ�����κ���y=����x��m��2+m2+1�����ֵ4����ʵ��m��ֵΪ��������
A. ��2 B. 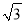 ��-
��-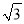 C. 2��-
C. 2��-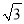 D. 2��
D. 2��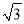 ��-
��-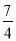
 C
��������������ø������ߵĶԳ���Ϊx=m.
�ٵ�-2��m��1ʱ,��ʱ���ֵΪ,��=4,
���m= (��ȥ)��m=-;
�ڵ�m>1ʱ,��ʱ��x=1ʱ,���������ֵ,����,
���m=2;
�۵�m<-2ʱ,��ʱx=-2���������ֵ,����,
���m= (��������,��ȥ).
��������,m= -��m=2.
����Cѡ������ȷ��.
C
��������������ø������ߵĶԳ���Ϊx=m.
�ٵ�-2��m��1ʱ,��ʱ���ֵΪ,��=4,
���m= (��ȥ)��m=-;
�ڵ�m>1ʱ,��ʱ��x=1ʱ,���������ֵ,����,
���m=2;
�۵�m<-2ʱ,��ʱx=-2���������ֵ,����,
���m= (��������,��ȥ).
��������,m= -��m=2.
����Cѡ������ȷ��. 
