题目内容
4.已知在矩形ABCD中,BE平分∠ABC交矩形一边于点E,若BD=8,∠EBD=15°,则AB=4或4$\sqrt{3}$.分析 画出图形,分两种情形讨论①点E在AD边上,②点E在AD延长线时,分别求出AB即可
解答 解:如图,①当点E在AD上时,∵四边形ABCD是矩形,
∴∠ABC=90°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=45°,
∵∠EBD=45°,
∴∠ABD=60°,
∴∠ADB=30°,
∵BD=8,
∴AB=$\frac{1}{2}$BD=4,
②当点E在AD的延长线上时,
在Rt△ABD′中,∵BD′=8,∠ABD′=30°,
∴AB=BD′•cos30°=4$\sqrt{3}$,
故答案为4或4$\sqrt{3}$.
点评 本题考查矩形的性质、角平分线的性质、直角三角形中30度角所对的直角边等于斜边的一半等知识,解题的关键是理解题意正确画出图形,注意不能漏解,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 如图,正方形ABCD由四个矩形构成,根据图形,写出一个含有a和b的正确的等式是( )
如图,正方形ABCD由四个矩形构成,根据图形,写出一个含有a和b的正确的等式是( )
 如图,正方形ABCD由四个矩形构成,根据图形,写出一个含有a和b的正确的等式是( )
如图,正方形ABCD由四个矩形构成,根据图形,写出一个含有a和b的正确的等式是( )| A. | a2-b2=(a+b)(a-b) | B. | a2+b2=(a+b)(a-b) | ||
| C. | (a+b)2=a2+b2 | D. | a2+b2+ab+ab=(a+b)(a+b) |
 如图,已知菱形ABCD中,∠ABD=70°,则∠ABC=140°.
如图,已知菱形ABCD中,∠ABD=70°,则∠ABC=140°. 某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种与某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题:
某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种与某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题: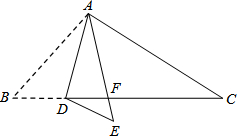 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F,则∠AFC=110°.
如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F,则∠AFC=110°.