题目内容
15．
如图，正方形ABCD由四个矩形构成，根据图形，写出一个含有a和b的正确的等式是（ ）| A． | a2-b2=（a+b）（a-b） | B． | a2+b2=（a+b）（a-b） | ||
| C． | （a+b）2=a2+b2 | D． | a2+b2+ab+ab=（a+b）（a+b） |
分析 根据图形，将正方形ABCD的面积运用两种不同的方式表达出来，即可得到等式a2+b2+ab+ab=（a+b）（a+b）．
解答 解：由图可得，
正方形ABCD的面积=（a+b）（a+b），
正方形ABCD的面积=a2+ab+ab+b2，
∴a2+b2+ab+ab=（a+b）（a+b）．
故选：D．
点评 本题主要参考了完全平方公式的几何背景，解决问题的关键是：用大正方形的面积等于边长为a和边长为b的两个正方形与两个长宽分别是a，b的长方形的面积的和作为相等关系．
练习册系列答案
阅读快车系列答案
相关题目
3．小英把1000元钱按年利率2.45%存入银行，存期为两年，那么计算到期时她可以从银行取回多少钱（不计利息税），列式正确的是（ ）
| A． | 1000×2.45%×2 | B． | （1000×2.45%+1000）×2 | ||
| C． | 1000×2.45%+1000 | D． | 1000×2.45%×2+1000 |
10．下列根式中，属于最简二次根式的是（ ）
| A． | $\sqrt{17}$ | B． | $\sqrt{12}$ | C． | $\sqrt{2.4}$ | D． | $\sqrt{\frac{1}{3}}$ |
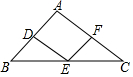如图，△ABC的边AB、BC、CA的中点分别是D、E、F，已知AB=8，AC=10，则四边形ADEF的周长是（ ）