Question

2．如图，在?ABCD中，AB=2cm，BC=3cm，∠B、∠C的平分线分别交AD于E，F，连结BE、CE，两线交于点G
（1）求证：AE=DF；
（2）求EF的长；
（3）若FG=$\frac{1}{2}$cm，求?ABCD的面积．

Answer 1

分析 （1）只要证明AB=AE、DF=CD，即可解决问题．
（2）求出AF、DE，根据EF=AD-AF-DE即可解决问题．
（3）先求出CF的长，发现△FCD是等边三角形，求出高CN，即可解决问题．

解答 （1）证明：如图1中，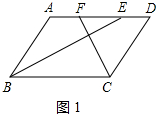

∵四边形ABCD是平行四边形，
∴AD∥BC，
∵BE平分∠ABC，CF平分∠BCD，
∴∠ABE=∠EBC=∠AEB，∠FCD=∠FCB=∠DFC，
∴AB=AE=2，DC=DF=2，
∴AE=DF．

（2）由（1）可知，AE=DF=2，
∵BC=AD=3，
∴AF=DE=1，
∴EF=AD-AE-DE=1．

（3）如图2中，作CN⊥AD于N．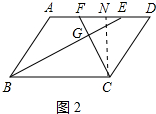

∵EF∥BC，
∴△EFG∽△BCG，
∴$\frac{EF}{BC}$=$\frac{FG}{GC}$，
∴$\frac{1}{3}$=$\frac{\frac{1}{2}}{CG}$，
∴CG=$\frac{3}{2}$，CF=FG+CG=2，
∴CF=DF=CD=2，
∴CN=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$，
∴S_{平行四边形ABCD}=BC×CN=3$\sqrt{3}$．

点评 本题考查四边形综合题、角平分线定义，等腰三角形的判定和性质、等边三角形的判定和性质等知识，解题的关键是灵活应用这些知识解决问题，学会添加常用辅助线，属于中考常考题型．