Question

7．如图，在△ABC中，∠C=90°，BC、AC、AB边的长分别记为a、b、c，点E是BC边上一个动点（点E与点B、C不重合），连接AE．已知a、b满足$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$，且c是不等式组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}＞x-3}\end{array}\right.$的最大整数解．
（1）求a、b、c的长．
（2）线段AE将△ABC分为△ABE和△ACE，若这两个三角形的周长相等，求CE的长．
（3）将△ACE沿直线AE折叠，使点C恰好落在AB边上的点C′处，求此时CE的长．（若需要，请自己画出符合题意的图形）

Answer 1

分析 （1）解方程组$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$与不等式组组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}＞x-3}\end{array}\right.$即可；（2）利用三角形的周长的定义与线段BC、BE、CE之间（BE=BC-CE）的关系分析求解；（3）由对称的性质得
AC=AC′，可求得BC′的长，再证明△BED∽△BC′A，利用相似三角形的性质即可求得CE的长．

解答 解：（1）∵a、b满足$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$，
∴解得：$\left\{\begin{array}{l}{a=8}\\{b=6}\end{array}\right.$
∵c是不等式组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}＞x-3}\end{array}\right.$的最大整数解，
解得：-4≤x＜11，
∴c=10．
即：a=8，b=6，c=10．
（2）∵C_△ABE=C_△ACE，
∴AC+EC+AE=AB+BE+AE，
又∵BE=BC-CE，
∴AC+EC+AE=AB+（BC-CE）+AE，
∴CE=AB-AC+（BC-CE），
    2CE=AB-AC+BC
      CE=$\frac{1}{2}$（10-6+8）=6
即：CE的长为6．
（3）如下图所示：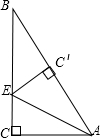

∵将△ACE沿直线AE折叠，点C恰好落在AB边上的点C′处，
∴∠ACE=∠EC′A=90°，AC=AC′，CE=C′E，
∴BC′=4，
在△BED和△BC′A中，$\left\{\begin{array}{l}{∠C′BE=∠CBA}\\{∠BC′E=∠BCA}\end{array}\right.$
∴△BED∽△BC′A，
∴$\frac{BD}{AB}=\frac{ED}{AC}$
即：$\frac{4}{10}=\frac{ED}{6}$，
∴CE=ED=$\frac{12}{5}$

点评 本题考查了解方程组、解不等式组、相似三角形的判定与性质等知识点，解题的关键是熟练掌握各个知识点及其之间的联系．