题目内容
20．
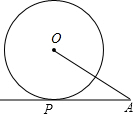如图，已知AP是⊙O的切线，切点为P，AP=3$\sqrt{3}$，∠PAO=30°，那么线段OA=6．
分析 连接OP，根据切线的性质得出∠OPA=90°，解直角三角形求出OA即可．
解答 解：连接OP，
∵AP是⊙O的切线，切点为P，
∴∠OPA=90°，
∵AP=3$\sqrt{3}$，∠PAO=30°，
∴OA=$\frac{AP}{cos30°}$=6，
故答案为：6．
点评 本题考查了切线的性质和解直角三角形的应用，能熟练掌握切线的性质定理是解此题的关键，注意：圆的切线垂直于过切点的半径．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
如图，已知正方形纸片ABCD的边长为8，⊙O的半径为2，圆心在正方形的中心上，将纸片按图示方式折叠，使EA恰好与⊙O相切于点A（△EFA与⊙O除切点外无重叠部分），延长FA交CD边于点G，则AG的长是$\frac{\sqrt{865}}{3}$．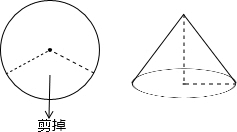
如图，若将半径为6cm的圆形纸片剪去$\frac{1}{3}$，剩下的部分围成一个圆锥的侧面，则围成圆锥的全面积为40π（cm2）．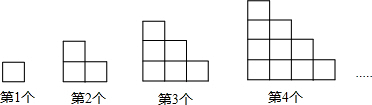
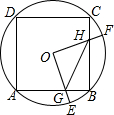如图，边长为4的正方形ABCD内接于点O，点E是$\widehat{AB}$上的一动点（不与A、B重合），点F是$\widehat{BC}$上的一点，连接OE、OF，分别与AB、BC交于点G，H，且∠EOF=90°，有以下结论：