题目内容
10. 如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A(△EFA与⊙O除切点外无重叠部分),延长FA交CD边于点G,则AG的长是$\frac{\sqrt{865}}{3}$.
如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A(△EFA与⊙O除切点外无重叠部分),延长FA交CD边于点G,则AG的长是$\frac{\sqrt{865}}{3}$.
分析 作FS⊥CD于点S,根据折叠得出FA=FA′,根据矩形的性质得出AF=SD,AD=FS;设AF=x,则A′F=DS=CG=x,GS=8-2x,FO=FA′+OA′=2+x,FG=2(2+x);根据勾股定理得出方程[2(2+x)]2=(8-2x)2+82,求出x,再根据勾股定理求出即可.
解答 解:如图,作FS⊥CD于点S,则AF=CG,
∵△AFE≌△A′FE,
∴FA=FA′,
∵四边形ADSF是矩形,
∴AF=SD,AD=FS;
设AF=x,则A′F=DS=CG=x,GS=8-2x,FO=FA′+OA′=2+x,FG=2(2+x);
∵FG2=GS2+FS2,
∴[2(2+x)]2=(8-2x)2+82,
解得x=$\frac{7}{3}$,
∴AF=CG=$\frac{7}{3}$,
DG=8-$\frac{7}{3}$=$\frac{17}{3}$,
∵四边形ABCD是正方形,
∴∠D=90°,
由勾股定理得:AG=$\sqrt{A{D}^{2}+D{G}^{2}}$=$\sqrt{{8}^{2}+(\frac{17}{3})^{2}}$=$\frac{\sqrt{865}}{3}$,
故答案为:$\frac{\sqrt{865}}{3}$.
点评 本题考查了正方形是中心对称图形,正方形的性质,勾股定理,折叠的性质的应用,能综合运用知识点进行推理和计算是解此题的关键,注意:圆的切线垂直于过切点的半径.

练习册系列答案
相关题目
18.某小区为了绿化环境,计划分两次购进A、B两种花草(两次购进的A、B两种花草价格均分别相同).购买数量和费用如表:
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,设购买A种花草x棵,购买费用为y元;
①写出y与x的函数关系式;
②请你给出一种费用最省的方案,并求出该方案所需费用.
| A | B | 费用(元) | |
| 第一次 | 30 | 15 | 675 |
| 第二次 | 12 | 5 | 265 |
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,设购买A种花草x棵,购买费用为y元;
①写出y与x的函数关系式;
②请你给出一种费用最省的方案,并求出该方案所需费用.
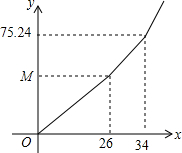 某市为鼓励居民节约用水,实行新的阶梯水价,即按用水量进行分段收费,阶段水价方案主要分为三档:
某市为鼓励居民节约用水,实行新的阶梯水价,即按用水量进行分段收费,阶段水价方案主要分为三档: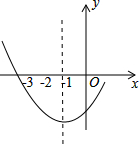 如图是二次函数y=ax2+bx-1图象的一部分,其对称轴为x=-1,且过点(-3,0),则(a+b+1)(2-a-b)=2.
如图是二次函数y=ax2+bx-1图象的一部分,其对称轴为x=-1,且过点(-3,0),则(a+b+1)(2-a-b)=2.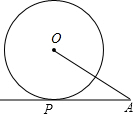 如图,已知AP是⊙O的切线,切点为P,AP=3$\sqrt{3}$,∠PAO=30°,那么线段OA=6.
如图,已知AP是⊙O的切线,切点为P,AP=3$\sqrt{3}$,∠PAO=30°,那么线段OA=6.