题目内容
12.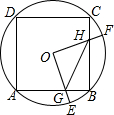 如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A、B重合),点F是$\widehat{BC}$上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A、B重合),点F是$\widehat{BC}$上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:①$\widehat{AE}$=$\widehat{BF}$;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+$\sqrt{2}$.
其中正确的是①②(把你认为正确结论的序号都填上).
分析 ①根据ASA可证△BOE≌△COF,根据全等三角形的性质得到BE=CF,根据等弦对等弧得到$\widehat{AE}$=$\widehat{BF}$,可以判断①;
②根据SAS可证△BOG≌△COH,根据全等三角形的性质得到∠GOH=90°,OG=OH,根据等腰直角三角形的判定得到△OGH是等腰直角三角形,可以判断②;
③通过证明△HOM≌△GON,可得四边形OGBH的面积始终等于正方形ONBM的面积,可以判断③;
④根据△BOG≌△COH可知BG=CH,则BG+BH=BC=4,设BG=x,则BH=4-x,根据勾股定理得到GH=$\sqrt{B{G}^{2}+B{H}^{2}}$=$\sqrt{{x}^{2}+(4-x)^{2}}$,可以求得其最小值,可以判断④.
解答 解:①如图所示,
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
在△BOE与△COF中,
$\left\{\begin{array}{l}{OB=OC}\\{∠BOE=∠COF}\\{OE=OF}\end{array}\right.$,
∴△BOE≌△COF,
∴BE=CF,
∴$\widehat{AE}$=$\widehat{BF}$,①正确;
②∵BE=CF,
∴△BOG≌△COH;
∵∠BOG=∠COH,∠COH+∠OBF=90°,
∴∠GOH=90°,OG=OH,
∴△OGH是等腰直角三角形,②正确.
③如图所示,
∵△HOM≌△GON,
∴四边形OGBH的面积始终等于正方形ONBM的面积,③错误;
④∵△BOG≌△COH,
∴BG=CH,
∴BG+BH=BC=4,
设BG=x,则BH=4-x,
则GH=$\sqrt{B{G}^{2}+B{H}^{2}}$=$\sqrt{{x}^{2}+(4-x)^{2}}$,
∴其最小值为4+2$\sqrt{2}$,D错误.
故答案为:①②.
点评 考查了圆的综合题,关键是熟练掌握全等三角形的判定和性质,等弦对等弧,等腰直角三角形的判定,勾股定理,面积的计算,综合性较强,有一定的难度.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | c<b<a | B. | c<a<b | C. | a<b<c | D. | b<a<c |
| A. | -$\frac{5}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{5}{2}$或$\frac{1}{2}$ | D. | 1 |
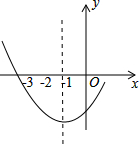 如图是二次函数y=ax2+bx-1图象的一部分,其对称轴为x=-1,且过点(-3,0),则(a+b+1)(2-a-b)=2.
如图是二次函数y=ax2+bx-1图象的一部分,其对称轴为x=-1,且过点(-3,0),则(a+b+1)(2-a-b)=2.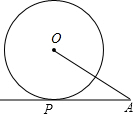 如图,已知AP是⊙O的切线,切点为P,AP=3$\sqrt{3}$,∠PAO=30°,那么线段OA=6.
如图,已知AP是⊙O的切线,切点为P,AP=3$\sqrt{3}$,∠PAO=30°,那么线段OA=6.