题目内容
10.商场某种商品平均每天可销售40件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价促销措施.经调查发现,每件商品每降价1元,商场平均每天可以多售出2件.设每件商品降价x元.请回答:(1)商场日销量将增加2x件,每件赢利50-x元(用含x的代数式表示).
(2)上述条件不变,销售正常的情况下,每件商品降价多少元时,商场日赢利可达2400元?
分析 (1)根据降价1元,可多售出2件,得出降价x元,可多售出2x件,盈利的钱数=原来的盈利-降低的钱数;
(2)根据每件商品的盈利×可卖出商品的件数=2400,列出方程进行求解即可.
解答 解:(1)∵降价1元,可多售出2件,
∴降价x元,可多售出2x件,
每件赢利的钱数=50-x;
故答案为2x;50-x;
(2)由题意得:(50-x)(40+2x)=2400,
解得:x1=10,x2=20,
∵该商场为了尽快减少库存,
∴降的越多,越吸引顾客,
∴x=20,
答:每件商品降价20元,商场日盈利可达2400元.
点评 此题考查了一元二次方程的应用;读懂题意,找出等量关系,列出方程是本题的关键;本题的等量关系是总利润=数量×每件的利润.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知a=($\frac{3}{5}$)${\;}^{-\frac{1}{3}}$,b=($\frac{5}{3}$)${\;}^{-\frac{1}{2}}$,c=($\frac{4}{3}$)${\;}^{-\frac{1}{2}}$,则a、b、c三个数的大小关系是( )
| A. | c<b<a | B. | c<a<b | C. | a<b<c | D. | b<a<c |
2.若关于x的方程x2+(m+1)x+$\frac{1}{2}$=0的一个实数根的倒数恰是它本身,则m的值是( )
| A. | -$\frac{5}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{5}{2}$或$\frac{1}{2}$ | D. | 1 |
15. 如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6cm,则菱形ABCD的周长是( )
如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6cm,则菱形ABCD的周长是( )
 如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6cm,则菱形ABCD的周长是( )
如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6cm,则菱形ABCD的周长是( )| A. | 12cm | B. | 48cm | C. | 30cm | D. | 24cm |
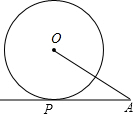 如图,已知AP是⊙O的切线,切点为P,AP=3$\sqrt{3}$,∠PAO=30°,那么线段OA=6.
如图,已知AP是⊙O的切线,切点为P,AP=3$\sqrt{3}$,∠PAO=30°,那么线段OA=6.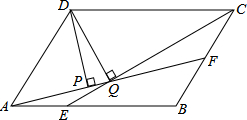 如图,平行四边形ABCD中,AB=3,BC=2,∠DAB=60°,E在AB上,且AE=$\frac{1}{2}$EB,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ的值为2$\sqrt{3}$:$\sqrt{13}$.
如图,平行四边形ABCD中,AB=3,BC=2,∠DAB=60°,E在AB上,且AE=$\frac{1}{2}$EB,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ的值为2$\sqrt{3}$:$\sqrt{13}$.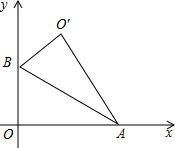 如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为($\sqrt{3}$,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$)..
如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为($\sqrt{3}$,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).. 如图,埃航MS804客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下500米的A点处测得俯角为45°的前下方海底有黑匣子信号发出,继续沿原方向直线航行2000米后到达B点,在B处测得俯角为60°的前下方海底有黑匣子信号发出,求海底黑匣子C点距离海面的深度(结果保留根号).
如图,埃航MS804客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下500米的A点处测得俯角为45°的前下方海底有黑匣子信号发出,继续沿原方向直线航行2000米后到达B点,在B处测得俯角为60°的前下方海底有黑匣子信号发出,求海底黑匣子C点距离海面的深度(结果保留根号).