��Ŀ����
4��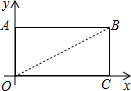 ��ƽ��ֱ������ϵ�У���A��x��y������A�䣨x�䣬y�䣩����x��=x+m��y��=y+n������A�䣨x+m��y+n�������ʾ��A����A���һ��ƽ�ƣ����磺��A��x��y������A�䣨x�䣬y�䣩����x��=x+1��y��=y-2�����ʾA����ƽ��1����λ��������ƽ��2����λ�õ���A�䣮
��ƽ��ֱ������ϵ�У���A��x��y������A�䣨x�䣬y�䣩����x��=x+m��y��=y+n������A�䣨x+m��y+n�������ʾ��A����A���һ��ƽ�ƣ����磺��A��x��y������A�䣨x�䣬y�䣩����x��=x+1��y��=y-2�����ʾA����ƽ��1����λ��������ƽ��2����λ�õ���A�䣮�����������壬̽���������⣺
��1����֪��A��x��y����A�䣨x-3��y�������߶�AA��ij�����3��
��2����֪��A��x��y����A�䣨x+2��y-1�������߶�AA��ij�����$\sqrt{5}$��
��3������AOCB��ƽ��ֱ������ϵ����ͼ��ʾ��A��0��2����C��4��0������A�䣨x�䣬y�䣩����x��=x+m��y��=y-2m��m��n��Ϊ���������ҵ�A�䣨x�䣬y�䣩�ڡ�OCB�У����������εıߣ�����m��ȡֵ��Χ��
���� ��1���ɵ�A��x��y����A�䣨x-3��y�������A����ƽ��3����λ�õ���A�䣬�����߶�AA��ij�����3��
��2���ɵ�A��x��y����A�䣨x+2��y-1�������A����ƽ��2����λ��������ƽ��1����λ�õ���A�䣬���ݹ��ɶ�����������߶�AA��ij��ȣ�
��3����tan��BOC=$\frac{BC}{OC}$=$\frac{2}{4}$=$\frac{1}{2}$��֪�������A�䣨x�䣬y�䣩�ڡ�OCB�У����������εıߣ�����ôy���$\frac{1}{2}$x�䣬��2-2m��$\frac{1}{2}$m�����m��$\frac{4}{5}$���ٸ���0��
x���4������⣮
��� �⣺��1����֪��A��x��y����A�䣨x-3��y�������߶�AA��ij�����3��
��2����֪��A��x��y����A�䣨x+2��y-1�������߶�AA��ij�����$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$��
��3����A��0��2������A�䣨x�䣬y�䣩��
��x��=x+m=m��y��=y-2m=2-2m��
��tan��BOC=$\frac{BC}{OC}$=$\frac{2}{4}$=$\frac{1}{2}$��
�൱��A�䣨x�䣬y�䣩�ڡ�OCB�У����������εıߣ�ʱ��y���$\frac{1}{2}$x�䣬
��2-2m��$\frac{1}{2}$m��
���m��$\frac{4}{5}$��
��0��m��4��
��$\frac{4}{5}$��m��4��
�ʴ�Ϊ3��$\sqrt{5}$��
���� ���⿼����������ͼ�α仯-ƽ�ƣ�����ƽ���е�ı仯���ɣ����������Ƽӣ����Ƽ������������Ƽӣ����Ƽ��ǽ���Ĺؼ���ͬʱ�����˹��ɶ�����һԪһ�β���ʽ��Ľⷨ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | ��x-4��2=19 | B�� | ��x-2��2=7 | C�� | ��x+2��2=7 | D�� | ��x+4��2=19 |
| A�� | $\sqrt{a+5}$ | B�� | $\sqrt{\frac{a}{3}}$ | C�� | $\sqrt{8}$ | D�� | $\sqrt{5{a^2}}$ |
| A�� | ���� | B�� | ����Ϊԭ����2�� | C�� | ����Ϊԭ����4�� | D�� | ��СΪԭ����$\frac{1}{2}$ |
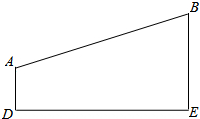 ��ͼ����֪AD��DE��BE��DE����DAB���ABE��ƽ���߽���C�㣮
��ͼ����֪AD��DE��BE��DE����DAB���ABE��ƽ���߽���C�㣮 һ���������ÿ���涼��һ�����֣���ƽ��չ��ͼ��ͼ��ʾ�����������к͡��֡���Ե����ǣ�������
һ���������ÿ���涼��һ�����֣���ƽ��չ��ͼ��ͼ��ʾ�����������к͡��֡���Ե����ǣ�������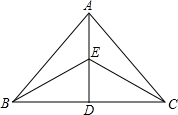 ��ͼ��ABC�У�D����BC�ϵĵ㣬E��AD���е㣬��BCE�������1�����ABC������ǣ�������
��ͼ��ABC�У�D����BC�ϵĵ㣬E��AD���е㣬��BCE�������1�����ABC������ǣ�������