题目内容

12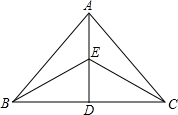．如图△ABC中，D点是BC上的点，E是AD的中点，△BCE的面积是1，则△ABC的面积是（　　）
A．1B．2C．4D．6

分析 如图，作辅助线，首先证明AM=2EF，借助三角形的面积公式求出△ABC与△BCE的面积之间的数量关系，即可解决问题．

解答 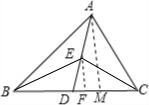解：如图，分别过点A、E作AM⊥BC、EF⊥DC；
则AM∥EF，
∴△ADM∽△EDF，$\frac{AM}{EF}=\frac{AD}{DE}$；
∵AE=DE，
∴AM=2EF（设EF为λ），
∴$\frac{{S}_{△ABC}}{{S}_{△BEC}}=\frac{\frac{1}{2}BC•2λ}{\frac{1}{2}BC•λ}=2$，而S△BCE=1，
S△ABC=2．
故选B．

点评 该题主要考查了三角形的面积公式及其应用问题；解题的关键是作辅助线，借助相似三角形的判定及其性质，求出△ABC与△BCE的高之间的数量关系．

练习册系列答案
相关题目
2．化简并计算：
（1）$\sqrt{\frac{32}{25x{\;}^{2}}}$     （2）$\sqrt{\frac{27xy{\;}^{2}}{x{\;}^{2}}}$ 
（3）$\sqrt{\frac{2{5}^{2}-7{\;}^{2}}{27}}$  （4）$\sqrt{\frac{m{\;}^{2}+6mn+9n{\;}^{2}}{m{\;}^{2}n{\;}^{4}}}$（m＞0，n＞0）
（5）$\frac{x}{\sqrt{98x}}$      （6）$\frac{\sqrt{a+b}}{\sqrt{a-b}$
（7）$\frac{1}{\sqrt{8（a+b）{\;}^{3}}}$．
3．定义：a是不为1的有理数，我们把$\frac{1}{1-a}$称为a的差倒数．如：2的差倒数是$\frac{1}{1-2}=-1$，-1的差倒数是$\frac{1}{{1-（{-1}）}}=\frac{1}{2}$．已知a1=-3，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数，…，依此类推，则a2011=-3．
20．如图，以AE为折痕折叠矩形ABCD的一边AD，使点D落在BC边的点F处，AF交BD于P点．
（1）求证：sin∠BAF=$\frac{BP}{PD}$；
（2）求证：PE⊥CD；
（3）在AD边上截取DG，使DG=CF，连接GE交BD于H，试判断△EFH的外接圆与CD的位置关系，证明你的结论．
7．计算：1-$\frac{{a}^{2}-81}{{a}^{2}+6a+9}$÷$\frac{{a}^{2}-9}{a+3}$．
17．等腰三角形的一个角为50°，则它的底角为（　　）
A．50°B．65°C．50°或65°D．80°
4．在平面直角坐标系中，点A（x，y），点A′（x′，y′），若x′=x+m，y′=y+n，即点A′（x+m，y+n），则表示点A到点A′的一个平移．例如：点A（x，y），点A′（x′，y′），若x′=x+1，y′=y-2，则表示A向右平移1个单位，再向下平移2个单位得到点A′．
根据上述定义，探究下列问题：
（1）已知点A（x，y），A′（x-3，y），则线段AA′的长度是3；
（2）已知点A（x，y），A′（x+2，y-1），则线段AA′的长度是$\sqrt{5}$；
（3）矩形AOCB在平面直角坐标系中如图所示，A（0，2），C（4，0），点A′（x′，y′），若x′=x+m，y′=y-2m（m，n均为正数），且点A′（x′，y′）在△OCB中（包括三角形的边），求m的取值范围．
1．某商品进价a元，标价b元，打八折销售后，利润为0.8b-a元．
2．下列多项式能进行因式分解的是（　　）
A．x2-yB．x2+1C．x2-6xD．x2+y+y2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网