题目内容
14.在“大课间”活动跳绳时,相同时间内小锌跳了90下,小婷跳了120下,已知小婷每分钟比小欣多跳20下,请问两人每分钟分别跳多少下?分析 小欣每分钟跳x下,那么小婷就跳(x+20)下,根据小欣跳了90下的时间=小婷跳了120下的时间,可列方程.
解答 解:设小欣每分钟跳x下,由题意得,
$\frac{120}{20+x}$=$\frac{90}{x}$,
解得 x=60.
经检验,x=60是原方程的解,符合实际意义,
所以小欣每分钟跳60个,小婷每分钟跳60+20=80(个).
答:小欣每分钟跳60下,小婷每分钟跳80个.
点评 本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.

练习册系列答案
相关题目
5.计算$\sqrt{{{(\;-4\;)}^2}}$的结果是( )
| A. | 16 | B. | 4 | C. | 2 | D. | -4 |
2.下列多项式能进行因式分解的是( )
| A. | x2-y | B. | x2+1 | C. | x2-6x | D. | x2+y+y2 |
9.已知y=$\sqrt{2x-5}$+$\sqrt{5-2x}$-3,则2xy的值为( )
| A. | $\frac{15}{2}$ | B. | 15 | C. | -$\frac{15}{2}$ | D. | -15 |
6.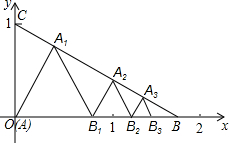 如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )
如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )
 如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )
如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )| A. | $\frac{\sqrt{3}}{{2}^{n}}$ | B. | $\frac{\sqrt{3}}{{2}^{n-1}}$ | C. | $\frac{3}{{2}^{n}}$ | D. | $\frac{3}{{2}^{n-1}}$ |
3.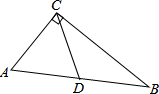 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=16,则CD的长是( )
如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=16,则CD的长是( )
 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=16,则CD的长是( )
如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=16,则CD的长是( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
 在平面直角坐标系中,点A(x,y),点A′(x′,y′),若x′=x+m,y′=y+n,即点A′(x+m,y+n),则表示点A到点A′的一个平移.例如:点A(x,y),点A′(x′,y′),若x′=x+1,y′=y-2,则表示A向右平移1个单位,再向下平移2个单位得到点A′.
在平面直角坐标系中,点A(x,y),点A′(x′,y′),若x′=x+m,y′=y+n,即点A′(x+m,y+n),则表示点A到点A′的一个平移.例如:点A(x,y),点A′(x′,y′),若x′=x+1,y′=y-2,则表示A向右平移1个单位,再向下平移2个单位得到点A′.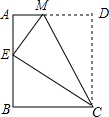 如图,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.
如图,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.