题目内容
1.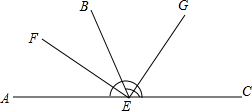 如图,A、E、C在同一直线上,EF、EG分别是∠AEB、∠BEC的平分线,求∠GEF的度数,并写出∠BEF的余角.
如图,A、E、C在同一直线上,EF、EG分别是∠AEB、∠BEC的平分线,求∠GEF的度数,并写出∠BEF的余角.
分析 由角平分线的定义可知∠GEB=$\frac{1}{2}$∠CEB,∠BEF=$\frac{1}{2}$∠AEB,然后逆用乘法的分配律可知:$\frac{1}{2}$∠CEB+$\frac{1}{2}$∠AEB=$\frac{1}{2}$(∠CEB+∠AEB)=90°.
解答 解:∵EF是∠AEB的平分线,
∴∠GEB=$\frac{1}{2}$∠CEB.
∵EG是∠BEC的平分线,
∴∠BEF=$\frac{1}{2}$∠AEB.
∴∠GEB=∠GEB+∠BEF
=$\frac{1}{2}$∠CEB+$\frac{1}{2}$∠AEB
=$\frac{1}{2}$(∠CEB+∠AEB)
=$\frac{1}{2}$×180°
=90.
点评 本题主要考查的是平分线的定义,逆用乘法分配律以及角的和差关系求得∠GEB=$\frac{1}{2}$(∠CEB+∠AEB)是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
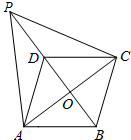 如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.
如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.