题目内容
8.△ABC中,∠ACB=90°,CD⊥AB于D,若AD=9,CD=6,则tan∠BCD=$\frac{2}{3}$.分析 根据三角形内角和定理证明∠A=∠BCD,再根据三角函数定义即可求解.
解答 解: ∵△ABC中,∠ACB=90°,CD⊥AB于D,
∵△ABC中,∠ACB=90°,CD⊥AB于D,
∴∠BCD+∠ACD=90°,∠ACD+∠90°,
∴∠A=∠BCD,
∴tan∠BCD=tanA=$\frac{CD}{AD}$=$\frac{6}{9}$=$\frac{2}{3}$.
故答案是:$\frac{2}{3}$.
点评 本题考查了三角函数的定义和性质,正确证明∠A=∠BCD是关键.

练习册系列答案
相关题目
18.在△ABC中,点D为边AC上的一点,∠DBC=∠A,BC=$\sqrt{6}$,AC=3,则CD的长为( )
| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
13.已知ac2=bc2,下列等式一定成立的是( )
| A. | 2ac2-1=bc2-2 | B. | ac=bc | C. | a=b | D. | ac2+1=bc2-1 |




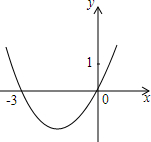 如图,已知二次函数y=ax2+bx+c的图象,确定下各式的符号:
如图,已知二次函数y=ax2+bx+c的图象,确定下各式的符号: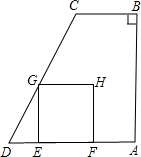 如图,梯形ABCD中,CB∥DA,∠ABC=90°,BA=AD=4,BC=2.动点E从点D出发,以每秒1个单位的速度沿线段DA运动,到点A停止,过点E作EG⊥AD交折线D-C-B于点G,以GE为一边向右作正方形GEFH.设运动时间为t(秒),正方形GEFH与梯形ABCD重叠面积为S(平方单位).
如图,梯形ABCD中,CB∥DA,∠ABC=90°,BA=AD=4,BC=2.动点E从点D出发,以每秒1个单位的速度沿线段DA运动,到点A停止,过点E作EG⊥AD交折线D-C-B于点G,以GE为一边向右作正方形GEFH.设运动时间为t(秒),正方形GEFH与梯形ABCD重叠面积为S(平方单位).