题目内容
17.1×3+1=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52…(1)根据以上等式,你发现了什么规律?用含正整数n的式子表示;
(2)利用发现的规律求1999×2001+1的值.
分析 (1)等式的左边是相差为2的两个数相乘,再加上1;右边是两个数的平均数的平方.根据这一规律用字母表示即可;
(2)利用发现的规律求解即可.
解答 解:(1)∵1×3+1=22;
2×4+1=9=32;
3×5+1=16=42;
4×6+1=25=52;
…
∴用含正整数n的式子表示为n(n+2)+1=(n+1)2.
(2)1999×2001+1=20002=4000000.
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律,解决问题.

练习册系列答案
相关题目
 如图.在Rt△ABC中,∠C=90°,BC=$\sqrt{3}$,CD⊥AB,垂足为D,AD=2,求AB的长和tanA的值.
如图.在Rt△ABC中,∠C=90°,BC=$\sqrt{3}$,CD⊥AB,垂足为D,AD=2,求AB的长和tanA的值.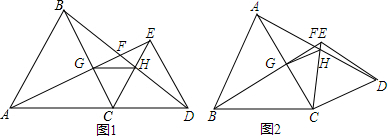
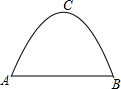 如图所示,某工厂大门是一抛物线形水泥建筑物,大门地面宽AB=4m,顶部C离地面高度为4m,现有一辆满载货物的汽车欲通过大门,货物顶部距离地面2m,装货宽度为2.5m,试判断这辆汽车能否顺利通过大门?通过计算说明.
如图所示,某工厂大门是一抛物线形水泥建筑物,大门地面宽AB=4m,顶部C离地面高度为4m,现有一辆满载货物的汽车欲通过大门,货物顶部距离地面2m,装货宽度为2.5m,试判断这辆汽车能否顺利通过大门?通过计算说明.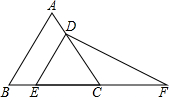 如图,已知△ABC是等边三角形,点D在AC上,且DE∥AB,DF⊥DE,交BC的延长线于点F,求证:CD=CF.
如图,已知△ABC是等边三角形,点D在AC上,且DE∥AB,DF⊥DE,交BC的延长线于点F,求证:CD=CF.