题目内容
3.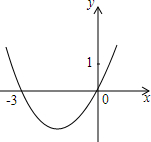 如图,已知二次函数y=ax2+bx+c的图象,确定下各式的符号:
如图,已知二次函数y=ax2+bx+c的图象,确定下各式的符号:(1)a>0;
(2)b>0;
(3)c=0;
(4)-$\frac{b}{2a}$<0;
(5)a+b+c>0;
(6)a-b+c<0.
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答  解:(1)如图所示,抛物线开口方向向上,则a>0.
解:(1)如图所示,抛物线开口方向向上,则a>0.
(2)如图所示,对称轴在y轴的左侧,则a、b同号,即b>0;
(3)如图所示,抛物线与y的交点是原点,则c=0;
(4)如图所示,对称轴在y轴的左侧,则-$\frac{b}{2a}$<0;
(5)如图所示,当x=1时,y>0,即a+b+c>0;
(6)如图所示,当x=-1时,y<0,即a-b+c<0.
故答案是:>;>;=;<;>;<.
点评 主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
11.有某种规律的一列数:20+0.5,30+1,40+1.5…,其中第五个数是( )
| A. | 50+2 | B. | 60+2.5 | C. | 60+2 | D. | 70+3 |
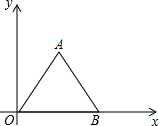 在平面直角坐标中.等边△OAB的OB在x轴上,0B=b,满足${a}^{2}-10a+25+\sqrt{b-4}=0$,D(a,0)
在平面直角坐标中.等边△OAB的OB在x轴上,0B=b,满足${a}^{2}-10a+25+\sqrt{b-4}=0$,D(a,0)