题目内容
6.解下列方程:①x2+3x-4=0;
②6x2-x-12=0;
③3(x-5)2=2(5-x);
④3x2+5(2x+1)=0.
分析 ①利用因式分解法解方程;
②利用因式分解法解方程;
③先移项得到3(x-5)2+2(x-5)=0,然后利用因式分解法解方程;
④先把方程整理为一般式,然后利用求根公式法解方程.
解答 解:①(x+4)(x-1)=0,
x+4=0或x-1=0,
所以x1=-4,x2=1;
②(2x-3)(3x+4)=0,
2x-3=0或3x+4=0,
所以x1=$\frac{3}{2}$,x2=-$\frac{4}{3}$;
③3(x-5)2+2(x-5)=0,
(x-5)(3x-15+2)=0,
x-5=0或3x-15+2=0,
所以x1=5,x2=$\frac{13}{3}$;
④3x2+10x+5=0,
△=102-4×3×5=40,
x=$\frac{-10±\sqrt{40}}{2×3}$=$\frac{-5±\sqrt{10}}{3}$
所以x1=$\frac{-5+\sqrt{10}}{3}$,x2=$\frac{-5-\sqrt{10}}{3}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了公式法解一元二次方程.

练习册系列答案
相关题目
 如图,EF过△ABC的一个顶点A,且EF∥BC,如果∠B=40°,∠2=75°,那么∠1、∠3、∠C各是多少度,并说明依据?
如图,EF过△ABC的一个顶点A,且EF∥BC,如果∠B=40°,∠2=75°,那么∠1、∠3、∠C各是多少度,并说明依据?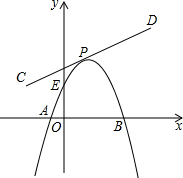 如图,形状不变的一条抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于E点,其顶点P在线段CD上移动,线段CD的解析式y=$\frac{3}{4}$x+$\frac{7}{4}$(-1≤x≤3),当顶点P从C点移动到D点时,求E点走过的路径长度.
如图,形状不变的一条抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于E点,其顶点P在线段CD上移动,线段CD的解析式y=$\frac{3}{4}$x+$\frac{7}{4}$(-1≤x≤3),当顶点P从C点移动到D点时,求E点走过的路径长度.