题目内容
1．先化简，再求值：（$\frac{x-1}{x}$-$\frac{x-2}{x+1}$）÷$\frac{2{x}^{2}-x}{{x}^{2}+2x+1}$，其中x=$\sqrt{3}$．分析 先根据分式混合运算的法则把原式进行化简，再把x的值代入进行计算即可．
解答 解：原式=$\frac{{x}^{2}-1-{x}^{2}+2x}{x（x+1）}$÷$\frac{x（2x-1）}{（x+1）^{2}}$
=$\frac{2x-1}{x（x+1）}$•$\frac{（x+1）^{2}}{x（2x-1）}$
=$\frac{x+1}{{x}^{2}}$，
当x=$\sqrt{3}$时，原式=$\frac{\sqrt{3}+1}{3}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
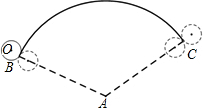如图，若弧BC的半径AB为12，圆心角为120°，半径为2的⊙O，从弧BC的一个端点B（切点）开始沿弧滚动到另一个端点C（切点），则⊙O需要转动2周．
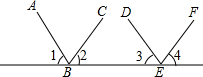完成下列推理说明：
如图，设置A、B的转盘分别被分成三个面积相等的扇形，A上的数字分别是1、6、8，B上的数字分别是4、5、7，现两人分别同时转动转盘，当转盘停止转动时，如果我们规定箭头所指较大数字一方获胜，那么你会选择哪个装置．请借助列表法或树状图法说明理由．