题目内容
16.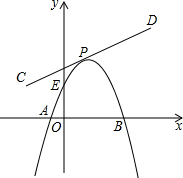 如图,形状不变的一条抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于E点,其顶点P在线段CD上移动,线段CD的解析式y=$\frac{3}{4}$x+$\frac{7}{4}$(-1≤x≤3),当顶点P从C点移动到D点时,求E点走过的路径长度.
如图,形状不变的一条抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于E点,其顶点P在线段CD上移动,线段CD的解析式y=$\frac{3}{4}$x+$\frac{7}{4}$(-1≤x≤3),当顶点P从C点移动到D点时,求E点走过的路径长度.
分析 设线段CD与y轴交点为F,分别求出P点位于C点和D点的抛物线解析式,进而求出抛物线与y轴的交点坐标,即可求出点P从C点到F点时和从F点到D点时E所走过的路径长度.
解答 解:设线段CD与y轴交点为F,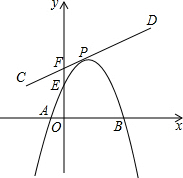
当顶点P位于C点时,
当x=-1,y=$\frac{3}{4}$x+$\frac{7}{4}$=1,即点C坐标为(-1,1),
此时抛物线解析式为y=-x2+2x,此时点B位于原点,
当点P移动到F点时,E点走过的路径长度为$\frac{7}{4}$,
点P移动到D点时,
当x=3时,y=$\frac{3}{4}$x+$\frac{7}{4}$=4,即点D的坐标为(3,4),
此时抛物线解析式为y=-x2+6x-5,此时点E位于y轴负半轴(0,-5),
此时E点走过的路径长度为$\frac{7}{4}$+5=$\frac{27}{4}$,
综上E点走过的路径长度为$\frac{7}{4}$+$\frac{27}{4}$=$\frac{17}{2}$.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是要分段讨论点E走路的路径,此题还要掌握二次函数的性质,此题有一定的难度.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
11.关于x的方程2x2+ax+b=0有两个不相等的实数根,且较小的根为2,则下列结论:①ab<-64;②|a|<|b|;③抛物线y=2x2+ax+b-1的顶点在第四象限.其中正确的结论是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
6.学校举行卫生大扫除,原来把七年(1)班分成两个劳动小组,第一组27人打扫操场,第二组18人打扫礼堂.后来根据工作需要,从七年(2)班调来15人,分配到第一组和第二组参加劳动,且要使第一组人数是第二组人数的2倍,那么分配到第一组、第二组各多少人?
(1)设分配到第一组x人,依题意填表:
(2)根据以上表格列出方程,求出分别调到第一组、第二组的人数.
(1)设分配到第一组x人,依题意填表:
| 第一组 | 第二组 | |
| 原来的人数 | 27 | 18 |
| 分配到的人数 | x | 15-x |
| 后来的人数 | 27+x | 33-x |

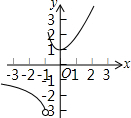
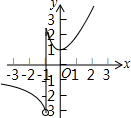
 如图,在直角坐标系中,已知A(3,0),点B为直线y=$\frac{\sqrt{3}}{3}$x上的一个动点,延长AB至C,使得AB=BC,过点C作CD⊥x轴于点D,交直线OB于点F,过点A作AE∥OB交直线CD于点E.
如图,在直角坐标系中,已知A(3,0),点B为直线y=$\frac{\sqrt{3}}{3}$x上的一个动点,延长AB至C,使得AB=BC,过点C作CD⊥x轴于点D,交直线OB于点F,过点A作AE∥OB交直线CD于点E.