题目内容
12.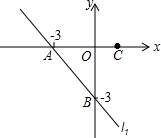 如图,在平面直角坐标系中,直线l1分别与x轴、y轴分别交于A、B两点,与抛物线y=x2+bx+c经过点A、B,且抛物线的对称轴为直线x=-1且过C点(点C点A的右侧).
如图,在平面直角坐标系中,直线l1分别与x轴、y轴分别交于A、B两点,与抛物线y=x2+bx+c经过点A、B,且抛物线的对称轴为直线x=-1且过C点(点C点A的右侧).(1)求直线l1与抛物线的解析式及点C的坐标;
(2)如果平行于x轴的动直线l2与抛物线交于点P,与直线l1交于点M,点N为OA的中点,那么是否存在这样的直线l2,使得△MON是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
分析 (1)根据直线l1分别与x轴、y轴分别交于A、B两点,求出直线l1的解析式,根据抛物线y=x2+bx+c经过点A、B,得出抛物线的解析式,由x2+2x-3=0得出点C的坐标,
(2)先求出AN=ON=1.5,过点N作M1N⊥x轴,交l1与点M1,根据∠OAB=45°,得出△M1ON是等腰三角形,根据点P的纵坐标为-1.5,得出x2+2x-3=-1.5求出点P的坐标,设ON的中点是D,过点D作DM2⊥x轴,交l1与M2,则M2N=M2O,△M2ON是等腰三角形,由x2+2x-3=-$\frac{9}{4}$得点P的坐标,当ON=OM时,OM与l1无交点,此时不存在直线l2使得△MON是等腰三角形.
解答 解:(1)设直线l1的解析式为y=kx+b,
$\left\{\begin{array}{l}{0=-3k+b}\\{-3=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=-3}\end{array}\right.$,
直线l1的解析式为y=-x-3,
∵抛物线y=x2+bx+c经过点A、B,
∴$\left\{\begin{array}{l}{0=9-3b+c}\\{-3=c}\end{array}\right.$,
解得;b=2,
∴抛物线的解析式为:y=x2+2x-3,
由x2+2x-3=0得:x1=1,x2=-3,
则点C的坐标为(-3,0),
(2)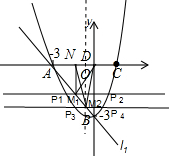 ∵点N为OA的中点,
∵点N为OA的中点,
∴AN=ON=1.5,
过点N作M1N⊥x轴,交l1与点M1,则M1的坐标为(-1.5,-1.5),
∵OA=OB,
∴∠OAB=45°,
∴AN=M1N,
∴△M1ON是等腰三角形,
∴当直线l2移动到点M1时△MON是等腰三角形,
∵l2∥x轴,
∴点P的纵坐标为-1.5,
由x2+2x-3=-1.5得:x1=$\frac{\sqrt{10}}{2}$-1,x2=-$\frac{\sqrt{10}}{2}$-1,
∴点P的坐标为P1($\frac{\sqrt{10}}{2}$-1,-1.5),P2=(-$\frac{\sqrt{10}}{2}$-1,-1.5),
设ON的中点是D,则D点的坐标是(-$\frac{3}{4}$,0),
过点D作DM2⊥x轴,交l1与M2,
则M2的坐标为;(-$\frac{3}{4}$,-$\frac{9}{4}$),M2N=M2O,△M2ON是等腰三角形,
由x2+2x-3=-$\frac{9}{4}$得:x1=$\frac{\sqrt{7}}{2}$-1,x2=-$\frac{\sqrt{7}}{2}$-1,
∴点P的坐标为P3(-$\frac{\sqrt{7}}{2}$-1,-$\frac{9}{4}$),P4=(-$\frac{\sqrt{7}}{2}$-1,-$\frac{9}{4}$),
当ON=OM时,OM与l1无交点,此时不存在直线l2使得△MON是等腰三角形.
点评 此题考查了二次函数的综合,用到的知识点是二次函数的图象与性质、等腰三角形的判定、一次函数的图象与性质,关键是根据题意画出图形,作出辅助线,注意求出所有符合要求的点.

| A. | 129 | B. | 120 | C. | 108 | D. | 96 |
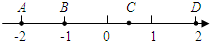 如图,数轴上用点A,B,C,D表示有理数,下列语句正确的有( )
如图,数轴上用点A,B,C,D表示有理数,下列语句正确的有( )①A点所表示的有理数大于B点所表示的有理数;
②B点所表示的有理数的绝对值大于C点所表示的有理数的绝对值;
③A点所表示的有理数与D点所表示的有理数和为0;
④C点所表示的有理数与B点所表示的有理数的乘积大于0.
| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
| A. | m3-m2=m | B. | -(-3)=3 | C. | (m+n)2=m2+n2 | D. | (3x)2=6x2 |
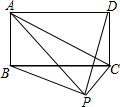 已知矩形ABCD,当点P在图中的位置时,则有结论( )
已知矩形ABCD,当点P在图中的位置时,则有结论( )| A. | S△PBC=S△PAC+S△PCD | B. | S△PBC=S△PAC-S△PCD | ||
| C. | S△PAB+S△PCD=$\frac{1}{2}$S矩形ABCD | D. | S△PAB+S△PCD<$\frac{1}{2}$S矩形ABCD |