题目内容
8. 如图,抛物线y=x2上的三点A、B、C的横坐标分别为a-d、a、a+d,试求△ABC的面积(用含有a,d的代数式表示).
如图,抛物线y=x2上的三点A、B、C的横坐标分别为a-d、a、a+d,试求△ABC的面积(用含有a,d的代数式表示).
分析 求得A、B、C的纵坐标,然后根据△ABC的面积等于大的梯形减去两个小的梯形的面积,从而得到三角形的面积的代数式.
解答 解;∵A、B、C的横坐标分别为a-d、a、a+d,
∴A、B、C的纵坐标分别为(a-d)2、a2、(a+d)2,
∴S△ABC=$\frac{1}{2}$[(a-d)2+(a+d)2](d-a+a+d)-$\frac{1}{2}$[(a-d)2+a2](d-a+a)-$\frac{1}{2}$[a2+(a+d)2](a+d-a)
=$\frac{1}{2}$d[(a-d)2+(a+d)2-2a2]
=d3.
点评 本题考查了二次函数图象上点的坐标特征以及梯形的面积,根据坐标特征求得纵坐标是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
20.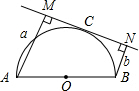 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )| A. | $\frac{3}{2}$(a+b) | B. | (a+b) | C. | $\frac{1}{2}$(a+b) | D. | $\frac{1}{3}$(a+b) |
18.一个长方形的长和宽分别是$3\sqrt{6}$、$2\sqrt{3}$,则它的面积是( )
| A. | $3\sqrt{6}+2\sqrt{3}$ | B. | 2(3$\sqrt{6}$+2$\sqrt{3}$) | C. | $18\sqrt{2}$ | D. | $6\sqrt{3}$ |
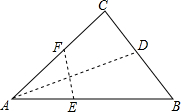 如图,在三角形纸片ABC中,∠BAC为锐角,AC=10cm,AB=15cm,按下列步骤折叠:第一次,过点A折叠,使C点落在AB边上,折痕交BC边于D点;第二次折叠,使点A与点D重合,折痕分别交AB、AC边于点E、F,展开后,连结DE、DF.
如图,在三角形纸片ABC中,∠BAC为锐角,AC=10cm,AB=15cm,按下列步骤折叠:第一次,过点A折叠,使C点落在AB边上,折痕交BC边于D点;第二次折叠,使点A与点D重合,折痕分别交AB、AC边于点E、F,展开后,连结DE、DF. 已知:如图,动点P在函数y=$\frac{k}{x}$(x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AF•BE的值为1,则k为$\frac{1}{2}$.
已知:如图,动点P在函数y=$\frac{k}{x}$(x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AF•BE的值为1,则k为$\frac{1}{2}$. 如图所示,若有两个等边三角形的顶点P1、P2都在函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点A1、A2在x轴上,直接写出点P2的坐标.
如图所示,若有两个等边三角形的顶点P1、P2都在函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点A1、A2在x轴上,直接写出点P2的坐标.