题目内容
12.已知,数轴上表示数0的点记为O,现有动点A从原点出发以0.5个单位长度/秒的速度向数轴负方向运动,同时动点B也从原点出发以2个单位长度/秒的速度向数轴正方向运动.(1)几秒钟后,两点相距15个单位长度?
(2)在(1)的条件下,若A、B两点到达相应的位置后,动点B立即按原速向数轴负方向运动,同时动点A以原速按原方向继续向前运动,问再经过几秒钟,OB=2OA?
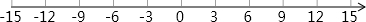
分析 (1)设x秒钟后,两点相距15个单位长度,由“距离=速度和×时间”可得出关于x的一元一次方程,解方程即可得出结论;
(2)设再经过y秒钟,OB=2OA,结合已知可知要分点A在O点的两边进行分析,由“路程=速度×时间”可得出关于y的一元一次方程,解方程即可得出结论.
解答 解:(1)设x秒钟后,两点相距15个单位长度,
由已知得:(0.5+2)x=15,
解得:x=6.
答:6秒钟后,两点相距15个单位长度.
(2)设再经过y秒钟,OB=2OA,
B点改方向时,点A所在的位置为-0.5×6=-3;
B点改方向时,点B所在的位置为2×6=12.
当OB=2OA时,分两种情况:
①B点在O点右侧时,如图1所示.
此时有12-2y=2(3+0.5y),
解得:y=2;
②B点在O点左侧时,如图2所示.
此时有2y-12=2(3+0.5y),
解得:y=18.
综上可知:再经过2或18秒钟,OB=2OA.
点评 本题考查了一元一次方程的应用以及数轴的相关知识,解题的关键是:(1)根据数量关系得出关于x的一元一次方程;(2)分类讨论,分别得出关于y的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,根据数量关系得出方程(或方程组)是关键.

练习册系列答案
相关题目
2. 如图,圆的半径等于正三角形ABC的高,此圆在沿底边AB滚动,切点为T,圆交AC、BC于M、N,则对于所有可能的圆的位置而言,$\widehat{MTN}$的度数为( )
如图,圆的半径等于正三角形ABC的高,此圆在沿底边AB滚动,切点为T,圆交AC、BC于M、N,则对于所有可能的圆的位置而言,$\widehat{MTN}$的度数为( )
 如图,圆的半径等于正三角形ABC的高,此圆在沿底边AB滚动,切点为T,圆交AC、BC于M、N,则对于所有可能的圆的位置而言,$\widehat{MTN}$的度数为( )
如图,圆的半径等于正三角形ABC的高,此圆在沿底边AB滚动,切点为T,圆交AC、BC于M、N,则对于所有可能的圆的位置而言,$\widehat{MTN}$的度数为( )| A. | 从30°到60°变动 | B. | 从60°到90°变动 | C. | 保持30°不变 | D. | 保持60°不变 |
20.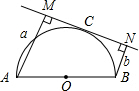 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )| A. | $\frac{3}{2}$(a+b) | B. | (a+b) | C. | $\frac{1}{2}$(a+b) | D. | $\frac{1}{3}$(a+b) |
1.下列计算正确的是( )
| A. | x6÷x3=x2 | B. | x2+x2=x4 | C. | 3a-a=2a | D. | x2+x2=x6 |
 如图所示,若有两个等边三角形的顶点P1、P2都在函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点A1、A2在x轴上,直接写出点P2的坐标.
如图所示,若有两个等边三角形的顶点P1、P2都在函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点A1、A2在x轴上,直接写出点P2的坐标.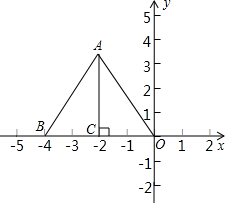 如图,把边长为4的等边三角形OAB置于平面直角坐标系中,点O与坐标原点重合,OB在x轴的负半轴上,点A在第二象限,AC⊥x轴于点C.
如图,把边长为4的等边三角形OAB置于平面直角坐标系中,点O与坐标原点重合,OB在x轴的负半轴上,点A在第二象限,AC⊥x轴于点C.