题目内容
5.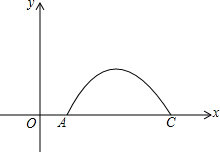 如图,一大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx+c,小王骑自行车从O匀速沿直线到拱梁一端A,再匀速通过拱梁部分的桥面AC,小王从O到A用了2秒,当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小王骑自行车通过拱梁部分的桥面AC供需26秒.
如图,一大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx+c,小王骑自行车从O匀速沿直线到拱梁一端A,再匀速通过拱梁部分的桥面AC,小王从O到A用了2秒,当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小王骑自行车通过拱梁部分的桥面AC供需26秒.
分析 根据二次函数图象具有对称性,由小王骑自行车行驶10秒时和20秒时拱梁的高度相同,可以得到抛物线的顶点的横坐标,根据小王从O到A用了2秒,可以得到点A的坐标,从而可以得到点B的坐标,进而得到AC的长度,从而可以计算出通过AC用的时间.
解答 解:设小王每秒行驶的速度为m,
则点A的坐标为(2m,0),
又∵当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,
∴抛物线顶点的横坐标是(10m+20m)÷2=15m,
∴点C的横坐标是:15m×2-2m=30m-2m=28m,
∴AC的长度是:28m-2m=26m,
∴小王骑自行车通过拱梁部分的桥面AC需要的时间是:26m÷m=26秒,
故答案是:26.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,根据二次函数图象具有对称性进行解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.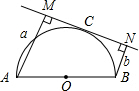 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )| A. | $\frac{3}{2}$(a+b) | B. | (a+b) | C. | $\frac{1}{2}$(a+b) | D. | $\frac{1}{3}$(a+b) |
10.将正整数1,2,3,4…按以下方式排列

根据排列规律,从2015到2017的箭头依次为( )

根据排列规律,从2015到2017的箭头依次为( )
| A. | ↓→ | B. | →↓ | C. | ↑→ | D. | →↑ |
14.下列计算正确的是( )
| A. | (x+5)(x-5)=x2-5 | B. | (x+2)(x-3)=x2-6 | C. | (x+1)(x-2)=x2-x-2 | D. | (x-1)(x+3)=x2-3x-3 |
15.下列计算正确的是( )
| A. | x•x2=x2 | B. | (a3)2=a5 | C. | a+2a=3a | D. | (ab)2=ab2 |
 已知:如图,动点P在函数y=$\frac{k}{x}$(x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AF•BE的值为1,则k为$\frac{1}{2}$.
已知:如图,动点P在函数y=$\frac{k}{x}$(x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AF•BE的值为1,则k为$\frac{1}{2}$.