题目内容
9.已知代数式$3a+\frac{1}{2}$与$2(a+\frac{1}{4})$.(1)当a为何值时,这两个代数式的值互为相反数?
(2)试比较这两个代数式的大小.
分析 (1)根据互为相反数两数之和为0列出方程,求出方程的解即可得到a的值;
(2)分三种情况考虑,当a=0,a>0,a<0,比较大小即可.
解答 解:(1)根据题意得:3a+$\frac{1}{2}$+2(a+$\frac{1}{4}$)=0,
去括号得:3a+$\frac{1}{2}$+2a+$\frac{1}{2}$=0,
移项合并得:5a=-1,
解得:a=-$\frac{1}{5}$;
(2)分3种情况考虑:
①当a>0时,3a+$\frac{1}{2}$>2(a+$\frac{1}{4}$);
②当a=0时,3a+$\frac{1}{2}$=2(a+$\frac{1}{4}$);
③当a<0时,3a+$\frac{1}{2}$<2(a+$\frac{1}{4}$).
点评 此题考查了解一元一次方程,以及相反数,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.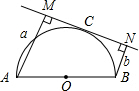 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )| A. | $\frac{3}{2}$(a+b) | B. | (a+b) | C. | $\frac{1}{2}$(a+b) | D. | $\frac{1}{3}$(a+b) |
14.下列计算正确的是( )
| A. | (x+5)(x-5)=x2-5 | B. | (x+2)(x-3)=x2-6 | C. | (x+1)(x-2)=x2-x-2 | D. | (x-1)(x+3)=x2-3x-3 |
1.下列计算正确的是( )
| A. | x6÷x3=x2 | B. | x2+x2=x4 | C. | 3a-a=2a | D. | x2+x2=x6 |
18.一个长方形的长和宽分别是$3\sqrt{6}$、$2\sqrt{3}$,则它的面积是( )
| A. | $3\sqrt{6}+2\sqrt{3}$ | B. | 2(3$\sqrt{6}$+2$\sqrt{3}$) | C. | $18\sqrt{2}$ | D. | $6\sqrt{3}$ |
19.关于反比例函数y=-$\frac{6}{x}$,下列说法正确的是( )
| A. | 图象过点(3,2) | B. | 图象在第一、三象限 | ||
| C. | 当x>0时,y随x的增大而减少 | D. | 当x<0时,y随x的增大而增大 |
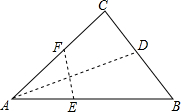 如图,在三角形纸片ABC中,∠BAC为锐角,AC=10cm,AB=15cm,按下列步骤折叠:第一次,过点A折叠,使C点落在AB边上,折痕交BC边于D点;第二次折叠,使点A与点D重合,折痕分别交AB、AC边于点E、F,展开后,连结DE、DF.
如图,在三角形纸片ABC中,∠BAC为锐角,AC=10cm,AB=15cm,按下列步骤折叠:第一次,过点A折叠,使C点落在AB边上,折痕交BC边于D点;第二次折叠,使点A与点D重合,折痕分别交AB、AC边于点E、F,展开后,连结DE、DF.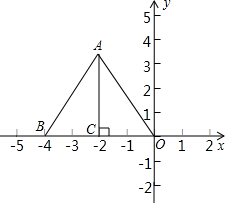 如图,把边长为4的等边三角形OAB置于平面直角坐标系中,点O与坐标原点重合,OB在x轴的负半轴上,点A在第二象限,AC⊥x轴于点C.
如图,把边长为4的等边三角形OAB置于平面直角坐标系中,点O与坐标原点重合,OB在x轴的负半轴上,点A在第二象限,AC⊥x轴于点C.