题目内容
 如图,△ABD和△ACE是△ABC外两个等腰直角三角形,∠BAD=∠CAE=90°.
如图,△ABD和△ACE是△ABC外两个等腰直角三角形,∠BAD=∠CAE=90°.(1)探索DC与BE的夹角的大小.
(2)取BC中点M,连MA,探讨MA与DE的位置关系.
考点:全等三角形的判定与性质,三角形中位线定理
专题:
分析:(1)根据等腰直角三角形性质可得AB=AD,AE=AC,易证∠DAC=∠BAE,即可证明△ABE≌△ADC,可得∠ABE=∠ADC,即可求得∠BOF=∠DAF=90°,即可解题.
(2)过B作BN∥AC,使得BN=AC,可得四边形ABNC为平行四边形,根据平行四边形的性质得到易证BN=AC=AE,∠BAC+∠ABN=180°,再根据∠BAC+∠DAE=180°即可求得∠DAE=∠ABN,即可证明△DAE≌△ABN,可得∠BAN=∠ADH,再根据∠DAH+∠BAN=90°,即可求得∠AHD=90°,即可解题.
(2)过B作BN∥AC,使得BN=AC,可得四边形ABNC为平行四边形,根据平行四边形的性质得到易证BN=AC=AE,∠BAC+∠ABN=180°,再根据∠BAC+∠DAE=180°即可求得∠DAE=∠ABN,即可证明△DAE≌△ABN,可得∠BAN=∠ADH,再根据∠DAH+∠BAN=90°,即可求得∠AHD=90°,即可解题.
解答:解:(1)如图,
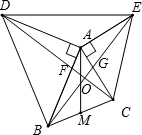
∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AE=AC,
又∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即:∠DAC=∠BAE,
在△ABE和△ADC中,
,
∴△ABE≌△ADC(SAS),
∴∠ABE=∠ADC,
又∵∠BFO=∠DFA,∠ADF+∠DFA=90°,
∴∠ABE+∠BFO=90°,
∴∠BOF=∠DAF=90°,即DC与BE的夹角为90°;
(2)过B作BN∥AC,使得BN=AC,则四边形ABNC为平行四边形,延长MA交DE于H,
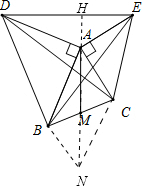
则BN=AC,
∵AC=AE,
∴BN=AE,
∵∠BAC+∠DAE=180°,∠BAC+∠ABN=180°,
∴∠DAE=∠ABN,
在△DAE和△ABN中,
,
∴△DAE≌△ABN,(SAS)
∴∠BAN=∠ADH,
∵∠DAH+∠BAN=90°,
∴∠DAH+∠ADH=90°,
∴∠AHD=90°,即AM⊥DE.

∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AE=AC,
又∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即:∠DAC=∠BAE,
在△ABE和△ADC中,
|
∴△ABE≌△ADC(SAS),
∴∠ABE=∠ADC,
又∵∠BFO=∠DFA,∠ADF+∠DFA=90°,
∴∠ABE+∠BFO=90°,
∴∠BOF=∠DAF=90°,即DC与BE的夹角为90°;
(2)过B作BN∥AC,使得BN=AC,则四边形ABNC为平行四边形,延长MA交DE于H,

则BN=AC,
∵AC=AE,
∴BN=AE,
∵∠BAC+∠DAE=180°,∠BAC+∠ABN=180°,
∴∠DAE=∠ABN,
在△DAE和△ABN中,
|
∴△DAE≌△ABN,(SAS)
∴∠BAN=∠ADH,
∵∠DAH+∠BAN=90°,
∴∠DAH+∠ADH=90°,
∴∠AHD=90°,即AM⊥DE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABE≌△ADC和△DAE≌△ABN是解题的关键.

练习册系列答案
相关题目
| cosβ•tanβ |
| sinβ•cotβ |
| A、sinβ | B、cosβ |
| C、tanβ | D、cotβ |
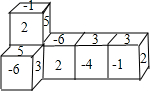 如图是一个由六个小正方体组成的几何体,每个小正方体的六个面上都写有-1,2,3,-4,5,-6,那么图中所有看不见的面上的数字和是( )
如图是一个由六个小正方体组成的几何体,每个小正方体的六个面上都写有-1,2,3,-4,5,-6,那么图中所有看不见的面上的数字和是( )| A、9 | B、8 | C、-15 | D、-13 |

 如图,在数轴上有两点A,B,它们所对应的数分别是a,8,(a<8),把线段AB的中点记为点C.
如图,在数轴上有两点A,B,它们所对应的数分别是a,8,(a<8),把线段AB的中点记为点C.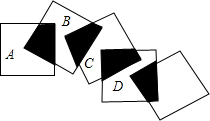 将5个边长都为1cm的正方形按如图所示的样子摆放,点A.B.C.D分别是四个正方形的中心,则图中四块阴影部分的面积的和为
将5个边长都为1cm的正方形按如图所示的样子摆放,点A.B.C.D分别是四个正方形的中心,则图中四块阴影部分的面积的和为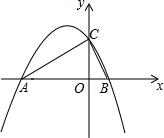 如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C(0,2),若∠ACB=90°,BC=
如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C(0,2),若∠ACB=90°,BC=