题目内容
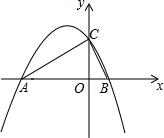 如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C(0,2),若∠ACB=90°,BC=
如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C(0,2),若∠ACB=90°,BC=| 5 |
(1)点A、B两点的坐标;
(2)二次函数的表达式.
考点:抛物线与x轴的交点
专题:
分析:(1)根据条件可求得OB和OA的长,可得到A、B两点的坐标;
(2)把A、B、C三点的坐标代入可求得a、b、c,可求得二次函数的表达式.
(2)把A、B、C三点的坐标代入可求得a、b、c,可求得二次函数的表达式.
解答:解:
(1)∵C(0,2),
∴OC=2,且BC=
,
在Rt△OBC中可求得OB=1,
∴B(1,0),
∵∠ACB=90°,
∴∠ACO+∠BCO=∠CAO+∠ACO=90°,
∴∠CAO=∠BCO,且∠AOC=∠COB,
∴△BCO∽△CAO,
∴
=
,即
=
,解得AO=4,
∴A(-4,0);
(2)把A、B、C三点的坐标代入二次函数的解析式可得
,解得
,
∴二次函数解析式为y=-
x2-
x+2.
(1)∵C(0,2),
∴OC=2,且BC=
| 5 |
在Rt△OBC中可求得OB=1,
∴B(1,0),
∵∠ACB=90°,
∴∠ACO+∠BCO=∠CAO+∠ACO=90°,
∴∠CAO=∠BCO,且∠AOC=∠COB,
∴△BCO∽△CAO,
∴
| CO |
| AO |
| BO |
| CO |
| 2 |
| AO |
| 1 |
| 2 |
∴A(-4,0);
(2)把A、B、C三点的坐标代入二次函数的解析式可得
|
|
∴二次函数解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题主要考查待定系数法求函数解析式,求得A、B两点的坐标是解题的关键,注意相似三角形的判定和性质的应用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
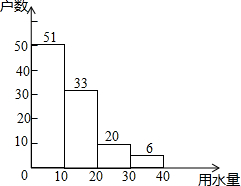 某小区300户家庭,从中随机抽取了100户,调查了他们5月份的用水量情况,结果如图所示.
某小区300户家庭,从中随机抽取了100户,调查了他们5月份的用水量情况,结果如图所示.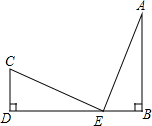 如图,CD⊥DB于D,AB⊥DB于B,CD=EB,AB=ED.求证:
如图,CD⊥DB于D,AB⊥DB于B,CD=EB,AB=ED.求证: 如图,△ABD和△ACE是△ABC外两个等腰直角三角形,∠BAD=∠CAE=90°.
如图,△ABD和△ACE是△ABC外两个等腰直角三角形,∠BAD=∠CAE=90°. 如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=2
如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=2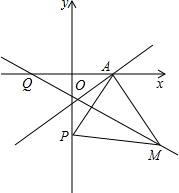 如图,点A、B的坐标分别为(a,0)、(b,0)且
如图,点A、B的坐标分别为(a,0)、(b,0)且 草原上有一个边长为5米的正方形木屋,A、B、C、D是木屋的角,在B点有一根木桩,用8米长的绳子把一匹马拴在木桩上,这匹马的活动范围是多少平方米?
草原上有一个边长为5米的正方形木屋,A、B、C、D是木屋的角,在B点有一根木桩,用8米长的绳子把一匹马拴在木桩上,这匹马的活动范围是多少平方米?