题目内容
在△ABC中，若|sinA﹣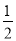
|+（
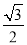﹣cosB）2=0，则∠C= 度．
120°
【解析】
试题分析：先根据非负数的性质，在△ABC中，|sinA﹣|+（﹣cosB）2=0，求出sinA=与cosB=，再根据特殊角三角函数值求出∠A=30°与∠B=30°，根据三角形内角和定理即可得出∠C=180°﹣30°﹣30°=120°．
练习册系列答案
相关题目
用“●”“■”“”分别表示三种不同的物体，如图所示，前两架天平保持平衡，若要使第三架天平也平衡，那么“？”处应放“■”的个数为（ ）
A．2个 B．3个 C．4个 D．5个
D
【解析】
试题分析：设“●”“■”“”分别为x、y、z，由图可知，
，解得x=2y，z=3y，
所以x+z=2y+3y=5y，即“■”的个数为5，
故选D． 向如图所示的正三角形区域扔沙包(区域中每一个小正三角形除颜色外完全相同)，假设沙包击中每一个小三角形是等可能的，扔沙包1次击中阴影区域的概率等于_______．
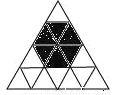
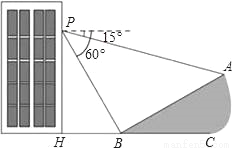
【解析】由图可以看出，一共有最小规格的正三角形16个，其中涂黑了的有6个.有等可能的情况之下，扔沙包1次击中阴影区域的概率等于．故答案为： . 如图所示，小明在大楼30米高（即PH=30米）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1：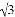
，点P、H、B、C、A在同一个平面上．点H、B、C在同一条直线上，且PH⊥HC．
（1）山坡坡角（即∠ABC）的度数等于_____度；
（2）求山坡A、B两点间的距离（结果精确到0.1米）．
（参考数据：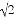
≈1.414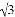，≈1.732）
30 (2) 34.6米
【解析】试题分析：（1）根据俯角以及坡度的定义即可求解；
（2）在直角△PHB中，根据三角函数即可求得PB的长，然后在直角△PBA中利用三角函数即可求解．
试题解析：（1）∵山坡的坡度i（即tan∠ABC）为1：．
∴tan∠ABC=，∴∠ABC=30°；∵从P点望山脚B处的俯角60°，
∴∠PBH=60°，∴∠ABP=180°﹣30°﹣60... 计算：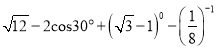 
．
．
【解析】试题分析：分别进行二次根式的化简、特殊角的三角函数值、零指数幂、负整数指数幂等运算，然后按照实数的运算法则计算即可．
试题解析：原式=
=． 在Rt△ABC中，∠C=90°，cosB=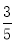
，AB=10cm，则BC的长度为( )
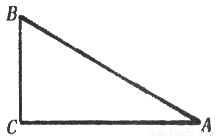
A. 6cm B. 7cm
C. 8cm D. 9cm
A
【解析】
试题分析：根据cosB=0.6可得：，则BC=6cm. 已知，如图△ABC中，三条高AD、BE、CF相交于点O．若∠BAC=60°，求∠BOC的度数．
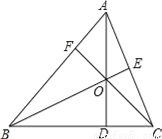
120°．
【解析】试题分析：先根据三角形的内角和定理求出∠ABE、∠ACF的度数，再根据三角形内角和定理求出∠EBO+∠FCB的度数，即可求出∠BOC．
试题解析：在△ABC中，∵∠BAC=60°，三条高AD、BE、CF相交于点O．
∴∠BEA=90°，∠CFA=90°，
∴∠ABE=30°，∠ACF=30°，
∴∠OBD+∠OCB=180°﹣∠BAC﹣∠OBD﹣∠... 下列命题中的真命题是（ ）
A. 锐角大于它的余角 B. 锐角大于它的补角
C. 钝角大于它的补角 D. 锐角与钝角之和等于平角
C
【解析】试题分析：A、锐角大于它的余角，不一定成立，故本选项错误；
B、锐角小于它的补角，故本选项错误；
C、钝角大于它的补角，本选项正确；
D、锐角与钝角之和等于平角，不一定成立，故本选项错误．
故选：C． 有一个小正方体，正方体的每个面分别标有1，2，3，4，5，6这六个数字．现在有甲、乙两位同学做游戏，游戏规则是：任意掷出正方体后，如果朝上的数字是6，甲是胜利者；如果朝上的数字不是6，乙是胜利者．你认为这个游戏规则对甲、乙双方公平吗？为什么？如果不公平，你打算怎样修改才能使游戏规则对甲、乙双方公平？
（1）这个游戏不公平．（2）游戏规则修改见解析（答案不唯一）
【解析】试题分析：分别求出甲胜利的概率和乙胜利的概率，比较大小看判断游戏是否公平，游戏规则修改只要是两人获胜的概率相等即可．
试题解析：（1）这个游戏不公平．因为正方体的每个面分别标有1，2，3，4，5，6这六个数字，其中数字6只有1个，也就是甲胜利的概率是；不是6的数字有5个，也就是说乙胜利的概率是，双方的胜利的机会不是均...