��Ŀ����
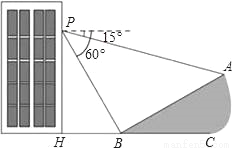
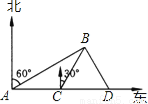
��ͼ��ʾ��С���ڴ�¥30�ߣ���PH=30�ף��Ĵ���P�����й۲⣬���ɽ����A���ĸ���Ϊ15�㣬ɽ��B���ĸ���Ϊ60�㣬��֪��ɽ�µ��¶�i����tan��ABC��Ϊ1��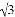 ����P��H��B��C��A��ͬһ��ƽ���ϣ���H��B��C��ͬһ��ֱ���ϣ���PH��HC��
����P��H��B��C��A��ͬһ��ƽ���ϣ���H��B��C��ͬһ��ֱ���ϣ���PH��HC��
��1��ɽ���½ǣ�����ABC���Ķ�������_____�ȣ�
��2����ɽ��A��B�����ľ��루�����ȷ��0.1�ף���
���ο����ݣ�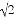 ��1.414��
��1.414��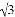 ��1.732��
��1.732��
 30 (2) 34.6��
�������������������1�����ݸ����Լ��¶ȵĶ��弴����⣻
��2����ֱ�ǡ�PHB�У��������Ǻ����������PB�ij���Ȼ����ֱ�ǡ�PBA���������Ǻ���������⣮
�����������1����ɽ�µ��¶�i����tan��ABC��Ϊ1����
��tan��ABC=�����ABC=30�㣻�ߴ�P����ɽ��B���ĸ���60�㣬
���PBH=60�㣬���ABP=180�㩁30�㩁60...
30 (2) 34.6��
�������������������1�����ݸ����Լ��¶ȵĶ��弴����⣻
��2����ֱ�ǡ�PHB�У��������Ǻ����������PB�ij���Ȼ����ֱ�ǡ�PBA���������Ǻ���������⣮
�����������1����ɽ�µ��¶�i����tan��ABC��Ϊ1����
��tan��ABC=�����ABC=30�㣻�ߴ�P����ɽ��B���ĸ���60�㣬
���PBH=60�㣬���ABP=180�㩁30�㩁60...
��ѧ���ϣ�����ʦ��ѧ����һ��������Ϸ������ѧ���������²�����м��㣺
������һ����λ��a����a����2���ټ���9�������õĺ��ٳ���2��
�ڰ�a����2���ټ���30�������õĺͳ���2��
�۰Ѣ����õĽ����ȥ�����õĽ��������Ϊ���Ľ����
����ʦ˵��ֻҪ����������Ľ�����Ҿ��ܲ³�����������λ��a�Ƕ��٣�
��ʱѧ��С������Ľ����69������ʦ�����³���������������λ����22��
��1���ú�a�Ĵ���ʽ��ʾ������ٵĽ���� ����ڵĽ���� ����۵Ľ����
��2����Сǿ�����������Ϸ�IJ�������˵�������Ľ����150����ôСǿ��������λ���Ƕ��٣�
 ��1��4a+18 a+15 3a+3��2��49
�������������������1�����ݢ٢ڢ۲����г�����ʽ������ɵó����ۣ�
��2����ϣ�1����֪3a��3��150����֮���ɵó����ۣ�
���������
��������
��1���������֪���ڢٲ�����Ľ��Ϊ��2(2a��9)��4a��18��
�ڢڲ�����Ľ��Ϊ�� (2a��30)��a��15��
�ڢ۲������Ϊ��(4a��18)��(a��15)...
��1��4a+18 a+15 3a+3��2��49
�������������������1�����ݢ٢ڢ۲����г�����ʽ������ɵó����ۣ�
��2����ϣ�1����֪3a��3��150����֮���ɵó����ۣ�
���������
��������
��1���������֪���ڢٲ�����Ľ��Ϊ��2(2a��9)��4a��18��
�ڢڲ�����Ľ��Ϊ�� (2a��30)��a��15��
�ڢ۲������Ϊ��(4a��18)��(a��15)... ���ж���ʽ�ij˷��У�������ƽ���ʽ������ǣ� ����
A.  B.
B.  C.
C.  D.
D. 
 C
�����������������A.(a+b)(b+a)��������ƽ���ʽ��
B.(?a+b)(a?b)�����Ϊ�෴����������ƽ���ʽ��
C. ����ʽ����һ����ȫ��ͬ����һ�Ϊ�෴��������ƽ���ʽ��
D. �������ͬ��������ƽ���ʽ.
��ѡC.
C
�����������������A.(a+b)(b+a)��������ƽ���ʽ��
B.(?a+b)(a?b)�����Ϊ�෴����������ƽ���ʽ��
C. ����ʽ����һ����ȫ��ͬ����һ�Ϊ�෴��������ƽ���ʽ��
D. �������ͬ��������ƽ���ʽ.
��ѡC. ��һ���ڴ��У�����50�������а���20��������20��������Ϊ����������һ���������ǰ���ĸ����ǣ� ��
A. 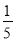 B.
B. 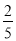 C.
C. 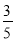 D.
D. 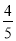
 C
���������ڴ��У�����50�������а���20������ô���ǰ��������30���������������ǰ���ĸ����ǣ���ѡC��
C
���������ڴ��У�����50�������а���20������ô���ǰ��������30���������������ǰ���ĸ����ǣ���ѡC�� 100����С��ͬ������1��100��ţ���������һ�����������ı���������ĸ����� �� ��
A.  B.
B.  C.
C.  D. ���϶�����
D. ���϶�����
 C
�������������1��100��100�����У����������ǣ�2��3 ��5��7��11��13��17��19��23��29��31 ��37��41��43��47��53��59��61��67��71��73��79��83��89��97����25�������������ı���������ĸ����ǣ� ��ѡC��
C
�������������1��100��100�����У����������ǣ�2��3 ��5��7��11��13��17��19��23��29��31 ��37��41��43��47��53��59��61��67��71��73��79��83��89��97����25�������������ı���������ĸ����ǣ� ��ѡC�� ��ͼ��ʾ��ij������11ʱ30����A���۲⺣��B�ڱ�ƫ��60�㷽�ô���ÿСʱ10������ٶȺ��е�C�����ٹ۲⺣��B�ڱ�ƫ��30�㷽������ͬ�����ٶȼ������е�D�����ٹ۲⺣���ڱ�ƫ��30�㷽���ִ�����C��ʱǡ���뺣��B���20�������ȷ���ִ�����C����D����ʱ�䣮
 �ִ�����C����ʱ��Ϊ13ʱ30�֣�����D����ʱ��15ʱ30��
��������������������ȸ�������ó���BAC=30�㣬��BCD=60�㣬�Ӷ��ó���BAC=��CBA=30�㣬��AC=BC����������ó���BDC=60�㣬�õ���BCDΪ�ȱ������Σ���BC=AC=CD=BD=20���Ӷ��������A�㵽��C�����õ�ʱ��ʹ���C�㵽��D�����õ�ʱ��.
�������������A���۲⺣��B�ڱ�ƫ��60�㷽���...
�ִ�����C����ʱ��Ϊ13ʱ30�֣�����D����ʱ��15ʱ30��
��������������������ȸ�������ó���BAC=30�㣬��BCD=60�㣬�Ӷ��ó���BAC=��CBA=30�㣬��AC=BC����������ó���BDC=60�㣬�õ���BCDΪ�ȱ������Σ���BC=AC=CD=BD=20���Ӷ��������A�㵽��C�����õ�ʱ��ʹ���C�㵽��D�����õ�ʱ��.
�������������A���۲⺣��B�ڱ�ƫ��60�㷽���... �ڡ�ABC�У���|sinA��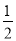 |+��
|+��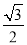 ��cosB��2=0�����C= �ȣ�
��cosB��2=0�����C= �ȣ�
 120��
��������
����������ȸ��ݷǸ��������ʣ��ڡ�ABC�У�|sinA��|+����cosB��2=0�����sinA=��cosB=���ٸ�����������Ǻ���ֵ�����A=30�����B=30�㣬�����������ڽǺͶ������ɵó���C=180�㩁30�㩁30��=120�㣮
120��
��������
����������ȸ��ݷǸ��������ʣ��ڡ�ABC�У�|sinA��|+����cosB��2=0�����sinA=��cosB=���ٸ�����������Ǻ���ֵ�����A=30�����B=30�㣬�����������ڽǺͶ������ɵó���C=180�㩁30�㩁30��=120�㣮 ��ͼ����ABC�У���A=100�㣬BI��CI�ֱ�ƽ�֡�ABC����ACB�����BIC=__����BM��CM�ֱ�ƽ�֡�ABC����ACB�����ƽ���ߣ����M=__��
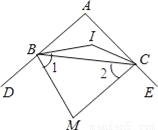
 140�㣻 40�㣮
���������ߡ�A=100�㣬
�ߡ�ABC+��ACB=180��?100��=80�㣬
��BI��CI�ֱ�ƽ�֡�ABC����ACB��
���IBC=��ABC����ICB=��ACB��
���IBC+��ICB=��ABC+��ACB= (��ABC+��ACB)= ��80��=40�㣬
���BIC=180��?(��IBC+��ICB)=180��?40��=140�㣬
�ߡ�...
140�㣻 40�㣮
���������ߡ�A=100�㣬
�ߡ�ABC+��ACB=180��?100��=80�㣬
��BI��CI�ֱ�ƽ�֡�ABC����ACB��
���IBC=��ABC����ICB=��ACB��
���IBC+��ICB=��ABC+��ACB= (��ABC+��ACB)= ��80��=40�㣬
���BIC=180��?(��IBC+��ICB)=180��?40��=140�㣬
�ߡ�... ����ͼ�ε�ȫ�ȣ�������������ȷ���ǣ���������
A. һ��ͼ�ξ�����ת��õ���ͼ�Σ���ԭ����ͼ��ȫ��
B. һ��ͼ�ξ������ĶԳƺ�õ���ͼ�Σ���ԭ����ͼ��ȫ��
C. һ��ͼ�ηŴ��õ���ͼ�Σ���ԭ����ͼ��ȫ��
D. һ��ͼ�ξ�����Գƺ�õ���ͼ�Σ���ԭ����ͼ��ȫ��
 C
��������A. һ��ͼ�ξ�����ת��õ���ͼ�Σ���ԭ����ͼ��ȫ�ȣ���ȷ�����������⣻
B. һ��ͼ�ξ������ĶԳƺ�õ���ͼ�Σ���ԭ����ͼ��ȫ�ȣ���ȷ�����������⣻
C. һ��ͼ�ηŴ��õ���ͼ�Σ���ԭ����ͼ�β�ȫ�ȣ��ʴ��������⣻
D. һ��ͼ�ξ�����Գƺ�õ���ͼ�Σ���ԭ����ͼ��ȫ�ȣ���ȷ�����������⣬
��ѡC.
C
��������A. һ��ͼ�ξ�����ת��õ���ͼ�Σ���ԭ����ͼ��ȫ�ȣ���ȷ�����������⣻
B. һ��ͼ�ξ������ĶԳƺ�õ���ͼ�Σ���ԭ����ͼ��ȫ�ȣ���ȷ�����������⣻
C. һ��ͼ�ηŴ��õ���ͼ�Σ���ԭ����ͼ�β�ȫ�ȣ��ʴ��������⣻
D. һ��ͼ�ξ�����Գƺ�õ���ͼ�Σ���ԭ����ͼ��ȫ�ȣ���ȷ�����������⣬
��ѡC. 
