题目内容
已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC=60°,求∠BOC的度数.
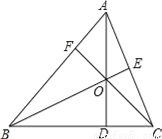
 120°.
【解析】试题分析:先根据三角形的内角和定理求出∠ABE、∠ACF的度数,再根据三角形内角和定理求出∠EBO+∠FCB的度数,即可求出∠BOC.
试题解析:在△ABC中,∵∠BAC=60°,三条高AD、BE、CF相交于点O.
∴∠BEA=90°,∠CFA=90°,
∴∠ABE=30°,∠ACF=30°,
∴∠OBD+∠OCB=180°﹣∠BAC﹣∠OBD﹣∠...
120°.
【解析】试题分析:先根据三角形的内角和定理求出∠ABE、∠ACF的度数,再根据三角形内角和定理求出∠EBO+∠FCB的度数,即可求出∠BOC.
试题解析:在△ABC中,∵∠BAC=60°,三条高AD、BE、CF相交于点O.
∴∠BEA=90°,∠CFA=90°,
∴∠ABE=30°,∠ACF=30°,
∴∠OBD+∠OCB=180°﹣∠BAC﹣∠OBD﹣∠...
练习册系列答案
相关题目
先化简,再求值: 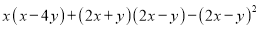 ,其中
,其中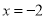 ,
, 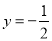 .
.
 【解析】试题分析:去括号,合并同类项,再把字母的值代入运算即可.
试题解析:原式,
,
当, 时,
原式.
【解析】试题分析:去括号,合并同类项,再把字母的值代入运算即可.
试题解析:原式,
,
当, 时,
原式. 100个大小相同的球,用1至100编号,任意摸出一个球,则摸出的编号是质数的概率是 ( )
A.  B.
B.  C.
C.  D. 以上都不对
D. 以上都不对
 C
【解析】解答:在1到100这100个数中,是质数的是:2,3 ,5,7,11,13,17,19,23,29,31 ,37,41,43,47,53,59,61,67,71,73,79,83,89,97,共25个,所以摸出的编号是质数的概率是, 故选C.
C
【解析】解答:在1到100这100个数中,是质数的是:2,3 ,5,7,11,13,17,19,23,29,31 ,37,41,43,47,53,59,61,67,71,73,79,83,89,97,共25个,所以摸出的编号是质数的概率是, 故选C. 在△ABC中,若|sinA﹣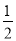 |+(
|+(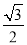 ﹣cosB)2=0,则∠C= 度.
﹣cosB)2=0,则∠C= 度.
 120°
【解析】
试题分析:先根据非负数的性质,在△ABC中,|sinA﹣|+(﹣cosB)2=0,求出sinA=与cosB=,再根据特殊角三角函数值求出∠A=30°与∠B=30°,根据三角形内角和定理即可得出∠C=180°﹣30°﹣30°=120°.
120°
【解析】
试题分析:先根据非负数的性质,在△ABC中,|sinA﹣|+(﹣cosB)2=0,求出sinA=与cosB=,再根据特殊角三角函数值求出∠A=30°与∠B=30°,根据三角形内角和定理即可得出∠C=180°﹣30°﹣30°=120°. 如果∠A为锐角,且cos A≤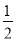 ,那么( )
,那么( )
A. 0°<∠A<60° B. 60°≤∠A<90° C. 0°<∠A≤30° D. 30°≤∠A<90°
 B
【解析】试题解析:当∠A是锐角时,余弦值随角度的增大而减小.
故选B.
B
【解析】试题解析:当∠A是锐角时,余弦值随角度的增大而减小.
故选B. 如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=__,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__.
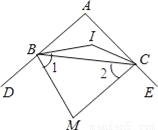
 140°; 40°.
【解析】∵∠A=100°,
∵∠ABC+∠ACB=180°?100°=80°,
∵BI、CI分别平分∠ABC,∠ACB,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠IBC+∠ICB=∠ABC+∠ACB= (∠ABC+∠ACB)= ×80°=40°,
∴∠BIC=180°?(∠IBC+∠ICB)=180°?40°=140°,
∵∠...
140°; 40°.
【解析】∵∠A=100°,
∵∠ABC+∠ACB=180°?100°=80°,
∵BI、CI分别平分∠ABC,∠ACB,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠IBC+∠ICB=∠ABC+∠ACB= (∠ABC+∠ACB)= ×80°=40°,
∴∠BIC=180°?(∠IBC+∠ICB)=180°?40°=140°,
∵∠... 满足下列条件的△ABC中,不是直角三角形的是( )
A.∠B+∠A=∠C B.∠A:∠B:∠C=2:3:5
C.∠A=2∠B=3∠C D.一个外角等于和它相邻的一个内角
 C
【解析】本题考查了直角三角形的判定
根据三角形的内角和是及邻补角是,对各选项进行分析即可。
A、∵∠B+∠A=∠C,∴∠C=90°,∴△ABC是直角三角形;
B、∵∠A:∠B:∠C=2:3:5,∴∠C=90°,∴△ABC是直角三角形;
C、∵∠A=2∠B=3∠C,∴∠A≠90°,∴△ABC不是直角三角形;
D、∵一个外角等于和它相邻的内角,∴每一个角等于90...
C
【解析】本题考查了直角三角形的判定
根据三角形的内角和是及邻补角是,对各选项进行分析即可。
A、∵∠B+∠A=∠C,∴∠C=90°,∴△ABC是直角三角形;
B、∵∠A:∠B:∠C=2:3:5,∴∠C=90°,∴△ABC是直角三角形;
C、∵∠A=2∠B=3∠C,∴∠A≠90°,∴△ABC不是直角三角形;
D、∵一个外角等于和它相邻的内角,∴每一个角等于90... 端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆粽、3只碱水粽、5只干肉粽,粽子除内部馅料不同外其它均相同,小颖随意吃一个,吃到红豆粽的概率是( )
A. 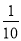 B.
B. 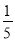 C.
C. 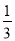 D.
D. 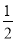
 B
【解析】试题分析:根据概率的定义,一共有10只粽子,其中红豆粽有2个,所以吃到红豆粽的概率是.
故选:B.
B
【解析】试题分析:根据概率的定义,一共有10只粽子,其中红豆粽有2个,所以吃到红豆粽的概率是.
故选:B. 
