题目内容
下列命题中的真命题是( )
A. 锐角大于它的余角 B. 锐角大于它的补角
C. 钝角大于它的补角 D. 锐角与钝角之和等于平角
 C
【解析】试题分析:A、锐角大于它的余角,不一定成立,故本选项错误;
B、锐角小于它的补角,故本选项错误;
C、钝角大于它的补角,本选项正确;
D、锐角与钝角之和等于平角,不一定成立,故本选项错误.
故选:C.
C
【解析】试题分析:A、锐角大于它的余角,不一定成立,故本选项错误;
B、锐角小于它的补角,故本选项错误;
C、钝角大于它的补角,本选项正确;
D、锐角与钝角之和等于平角,不一定成立,故本选项错误.
故选:C.
练习册系列答案
相关题目
下列多项式的乘法中,可以用平方差公式计算的是( ).
A.  B.
B.  C.
C.  D.
D. 
 C
【解析】试题解析:A.(a+b)(b+a),不符合平方差公式;
B.(?a+b)(a?b)两项都互为相反数,不符合平方差公式;
C. 二项式中有一项完全相同,另一项互为相反数,符合平方差公式;
D. 两项都不相同,不符合平方差公式.
故选C.
C
【解析】试题解析:A.(a+b)(b+a),不符合平方差公式;
B.(?a+b)(a?b)两项都互为相反数,不符合平方差公式;
C. 二项式中有一项完全相同,另一项互为相反数,符合平方差公式;
D. 两项都不相同,不符合平方差公式.
故选C. 在△ABC中,若|sinA﹣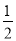 |+(
|+(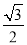 ﹣cosB)2=0,则∠C= 度.
﹣cosB)2=0,则∠C= 度.
 120°
【解析】
试题分析:先根据非负数的性质,在△ABC中,|sinA﹣|+(﹣cosB)2=0,求出sinA=与cosB=,再根据特殊角三角函数值求出∠A=30°与∠B=30°,根据三角形内角和定理即可得出∠C=180°﹣30°﹣30°=120°.
120°
【解析】
试题分析:先根据非负数的性质,在△ABC中,|sinA﹣|+(﹣cosB)2=0,求出sinA=与cosB=,再根据特殊角三角函数值求出∠A=30°与∠B=30°,根据三角形内角和定理即可得出∠C=180°﹣30°﹣30°=120°. 如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=__,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__.
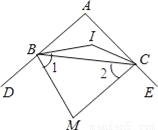
 140°; 40°.
【解析】∵∠A=100°,
∵∠ABC+∠ACB=180°?100°=80°,
∵BI、CI分别平分∠ABC,∠ACB,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠IBC+∠ICB=∠ABC+∠ACB= (∠ABC+∠ACB)= ×80°=40°,
∴∠BIC=180°?(∠IBC+∠ICB)=180°?40°=140°,
∵∠...
140°; 40°.
【解析】∵∠A=100°,
∵∠ABC+∠ACB=180°?100°=80°,
∵BI、CI分别平分∠ABC,∠ACB,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠IBC+∠ICB=∠ABC+∠ACB= (∠ABC+∠ACB)= ×80°=40°,
∴∠BIC=180°?(∠IBC+∠ICB)=180°?40°=140°,
∵∠... 下面四个图形中,线段BE是△ABC的高的图是( )
A. 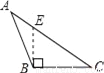 B.
B. 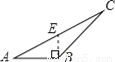 C.
C. 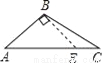 D.
D. 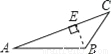
 D
【解析】试题分析:根据三角形高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高,再结合图形进行判断.
【解析】
线段BE是△ABC的高的图是选项D.
故选D.
D
【解析】试题分析:根据三角形高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高,再结合图形进行判断.
【解析】
线段BE是△ABC的高的图是选项D.
故选D. 满足下列条件的△ABC中,不是直角三角形的是( )
A.∠B+∠A=∠C B.∠A:∠B:∠C=2:3:5
C.∠A=2∠B=3∠C D.一个外角等于和它相邻的一个内角
 C
【解析】本题考查了直角三角形的判定
根据三角形的内角和是及邻补角是,对各选项进行分析即可。
A、∵∠B+∠A=∠C,∴∠C=90°,∴△ABC是直角三角形;
B、∵∠A:∠B:∠C=2:3:5,∴∠C=90°,∴△ABC是直角三角形;
C、∵∠A=2∠B=3∠C,∴∠A≠90°,∴△ABC不是直角三角形;
D、∵一个外角等于和它相邻的内角,∴每一个角等于90...
C
【解析】本题考查了直角三角形的判定
根据三角形的内角和是及邻补角是,对各选项进行分析即可。
A、∵∠B+∠A=∠C,∴∠C=90°,∴△ABC是直角三角形;
B、∵∠A:∠B:∠C=2:3:5,∴∠C=90°,∴△ABC是直角三角形;
C、∵∠A=2∠B=3∠C,∴∠A≠90°,∴△ABC不是直角三角形;
D、∵一个外角等于和它相邻的内角,∴每一个角等于90... 对于图形的全等,下列叙述不正确的是( )
A. 一个图形经过旋转后得到的图形,与原来的图形全等
B. 一个图形经过中心对称后得到的图形,与原来的图形全等
C. 一个图形放大后得到的图形,与原来的图形全等
D. 一个图形经过轴对称后得到的图形,与原来的图形全等
 C
【解析】A. 一个图形经过旋转后得到的图形,与原来的图形全等,正确,不符合题意;
B. 一个图形经过中心对称后得到的图形,与原来的图形全等,正确,不符合题意;
C. 一个图形放大后得到的图形,与原来的图形不全等,故错误,符合题意;
D. 一个图形经过轴对称后得到的图形,与原来的图形全等,正确,不符合题意,
故选C.
C
【解析】A. 一个图形经过旋转后得到的图形,与原来的图形全等,正确,不符合题意;
B. 一个图形经过中心对称后得到的图形,与原来的图形全等,正确,不符合题意;
C. 一个图形放大后得到的图形,与原来的图形不全等,故错误,符合题意;
D. 一个图形经过轴对称后得到的图形,与原来的图形全等,正确,不符合题意,
故选C. 长为l的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为__________.
 ≤x<
【解析】试题解析:∵围成两个全等的三角形可得两个三角形的周长相等,
∴可得
又因为x为最长边大于周长的,
综上可得
故答案为:
≤x<
【解析】试题解析:∵围成两个全等的三角形可得两个三角形的周长相等,
∴可得
又因为x为最长边大于周长的,
综上可得
故答案为: 
