题目内容
9.已知关于x的方程x2-(2k-1)x+k2-3=0有两个实根x1、x2.(1)求k的取值范围;
(2)若x1、x2满足x12+x22=5,求k的值.
分析 (1)由关于x的方程x2-(2k-1)x+k2-3=0有两个实根x1、x2,可得判别式△≥0,继而求得答案;
(2)由根与系数的关系可得x1+x2=2k-1,x1•x2=k2-3,又由x12+x22=(x1+x2)2-2x1•x2,即可求得答案.
解答 解:(1)∵关于x的方程x2-(2k-1)x+k2-3=0有两个实根x1、x2,
∴△=[-(2k-1)]2-4(k2-3)≥0,
解得:k≤$\frac{13}{4}$;
∴k的取值范围为:k≤$\frac{13}{4}$;
(2)∵x1+x2=2k-1,x1•x2=k2-3,x12+x22=5,
∴x12+x22=(x1+x2)2-2x1•x2=(2k-1)2-2(k2-3)=5,
解得:k=1.
点评 此题考查了根的判别式以及根与系数的关系.注意二次项系数为1,常用以下关系:x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.

练习册系列答案
相关题目
4.下列根式中属于最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{27}$ |
19.直线y=kx+b与y=mx+n交于点(2,-1).则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ |
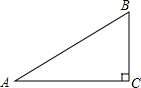 如图,△ABC中,∠C=90°,小王同学想作一个圆经过A、C两点,并且该圆的圆心到AB、AC距离相等,请你利用尺规作图的办法帮助小王同学确定圆心D.(不写作法,保留作图痕迹).
如图,△ABC中,∠C=90°,小王同学想作一个圆经过A、C两点,并且该圆的圆心到AB、AC距离相等,请你利用尺规作图的办法帮助小王同学确定圆心D.(不写作法,保留作图痕迹).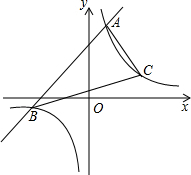 已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A,B两点,当x>1,时,y1>y2;当0<x<1时,y1<y2.
已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A,B两点,当x>1,时,y1>y2;当0<x<1时,y1<y2.
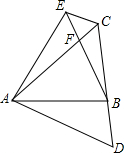 已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上
已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上