题目内容
19.直线y=kx+b与y=mx+n交于点(2,-1).则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解为( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ |
分析 根据二元一次方程组的解的定义知,该方程组的解就是组成方程组的两个二元一次方程的图象的交点.
解答 解:∵直线y=kx+b与y=mx+n交于点(2,-1),
∴方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
故选A.
点评 本题主要考查了一次函数与二元一次方程组的关系,关键是掌握方程组的解就是两函数图象的交点.

练习册系列答案
相关题目
7.将长为8cm,宽为6cm的矩形纸片ABCD折叠,使A与C重合,则折痕的长为( )
| A. | 6.5cm | B. | 7cm | C. | 7.5cm | D. | 8cm |
14.若x+y=m,xy=-3,则化简(x-3)(y-3)的结果是( )
| A. | 12 | B. | 3m+6 | C. | -3m-12 | D. | -3m+6 |
4.在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
| A. | 平均数为160 | B. | 中位数为158 | C. | 众数为158 | D. | 方差为20.3 |
6.下列式子中,正确的是( )
| A. | $\root{3}{-8}=-\root{3}{8}$ | B. | $-\sqrt{3.6}=-0.6$ | C. | $\sqrt{{{(-3)}^2}}=-3$ | D. | $\sqrt{36}=±6$ |
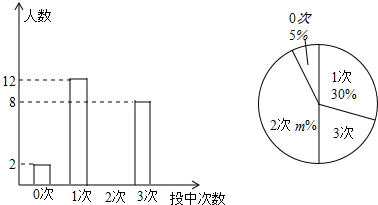
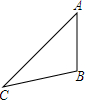 如图,△ABC中,∠B=100°,按要求完成画图并解答问题:
如图,△ABC中,∠B=100°,按要求完成画图并解答问题: