题目内容
17.为判断命题“有三条边相等且一组对角相等的四边形是菱形”的真假,数学课上,老师给出菱形ABCD,并作出了一个四边形ABC′D,具体作图过程如下:如图,在菱形ABCD中,①连接BD,以点B为圆心,以BD的长为半径作圆弧,交CD于点P;
②分别以B、D为圆心,以BC、PC的长为半径作圆弧,两弧交于点C′;
③连接BC′、DC′,得四边形ABC′D.
依据上述作图过程,解决以下问题:
求证:∠A=∠C′;AD=BC′.

分析 连接BP,由菱形的性质得出AD=BC,∠A=∠BCD,根据题意得出BC=B′C,BD=BP,DC′=PC,得出AD=BC′,由SSS证明△BPC≌△BDC′,得出对应角相等∠BCD=∠C′,即可得出∠A=∠C′.
解答 证明:连接BP,如图所示: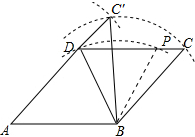
∵四边形ABCD是菱形,
∴AD=BC,∠A=∠BCD,
根据题意得:BC=B′C,BD=BP,DC′=PC,
∴AD=BC′,
在△BPC和△BDC′中,
$\left\{\begin{array}{l}{BC=BC′}&{\;}\\{BP=BD}&{\;}\\{PC=DC′}&{\;}\end{array}\right.$,
∴△BPC≌△BDC′(SSS),
∴∠BCD=∠C′,
∴∠A=∠C′.
点评 本题考查了菱形的判定与性质、全等三角形的判定与性质等知识;熟练掌握菱形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列计算正确的是( )
| A. | (y2)3÷y6=0 | B. | 16×2-4=2 | C. | (-a2b)3=a6b3 | D. | (-e2)2a=e4a |
5.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定满足( )
| A. | 对角线相等 | B. | 对角线互相平分 | ||
| C. | 对角线互相垂直 | D. | 对角线相等且相互平分 |
12.计算2$\sqrt{2}$-$\sqrt{2}$正确的是( )
| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | 3$\sqrt{2}$ |
7.将长为8cm,宽为6cm的矩形纸片ABCD折叠,使A与C重合,则折痕的长为( )
| A. | 6.5cm | B. | 7cm | C. | 7.5cm | D. | 8cm |
 如图,在菱形ABCD中,sin∠D=$\frac{4}{5}$,E,F分别是AB和CD上的点,BC=5,AE=CF=2,点P是线段EF上一点,则当△BPC是直角三角形时,CP的长为$\sqrt{5}$或4或$\frac{20}{11}$.
如图,在菱形ABCD中,sin∠D=$\frac{4}{5}$,E,F分别是AB和CD上的点,BC=5,AE=CF=2,点P是线段EF上一点,则当△BPC是直角三角形时,CP的长为$\sqrt{5}$或4或$\frac{20}{11}$.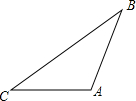 实践与操作:如图,在△ABC中,AB=3,∠C=30°.
实践与操作:如图,在△ABC中,AB=3,∠C=30°.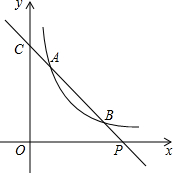 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C