题目内容
14.已知关于x的一元二次方程x2-3x+m-3=0.(1)若此方程有两个不相等的实数根,求m的取值范围;
(2)若此方程的两根互为倒数,求m的值.
分析 (1)由此方程有两个不相等的实数根,根据根的判别式,即可求得答案;
(2)由此方程的两根互为倒数,可得αβ=m-3=1,继而求得答案.
解答 解:(1)∵方程x2-3x+m-3=0有两个不相等的实数根,
∴△=(-3)2-4(m-3)>0,
解得:m<$\frac{21}{4}$;
∴m的取值范围为:m<$\frac{21}{4}$;
(2)设此方程的两个根分别为:α,β,
∴α+β=3,αβ=m-3,
∵此方程的两根互为倒数,
∴αβ=m-3=1,
∴m=4.
点评 此题考查了根的判别式以及根与系数的关系.注意二次项系数为1,常用以下关系:x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
5.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定满足( )
| A. | 对角线相等 | B. | 对角线互相平分 | ||
| C. | 对角线互相垂直 | D. | 对角线相等且相互平分 |
19.下列各式计算正确的是( )
| A. | 2x•3x2=6x2 | B. | (-3a2b)2=6a4b2 | C. | -a2+2a2=a2 | D. | (a+b)(a-2b)=a2-2b2 |
3.对于近似数0.7048,下列说法中正确的是( )
| A. | 它的准确值x的范围是0.70475<x<0.70485 | |
| B. | 它有三个有效数字 | |
| C. | 对它四舍五入精确到百分位为0.71 | |
| D. | 用科学记数法表示它为7.048×10-1 |
4.在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
| A. | 平均数为160 | B. | 中位数为158 | C. | 众数为158 | D. | 方差为20.3 |
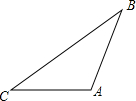 实践与操作:如图,在△ABC中,AB=3,∠C=30°.
实践与操作:如图,在△ABC中,AB=3,∠C=30°.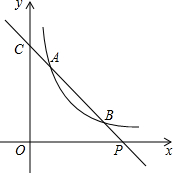 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C