题目内容
6.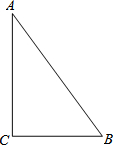 在直角三角形ABC中,∠C=90°,AB=5,BC=3.求斜边上的高线及中线的长.
在直角三角形ABC中,∠C=90°,AB=5,BC=3.求斜边上的高线及中线的长.
分析 根据直角三角形的性质可求斜边上中线的长,根据勾股定理求得AC的长,再根据面积公式求得斜边上的高线的长.
解答 解:∵在直角三角形ABC中,∠C=90°,AB=5,BC=3,
∴斜边上中线的长=$\frac{1}{2}$AB=2.5,
根据勾股定理,得:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4,
三角形的面积是$\frac{1}{2}$×3×4=6,
AB边上的高为$\frac{AC•BC}{AB}$=2.4.
点评 本题考查了勾股定理,熟练运用勾股定理进行计算.注意:直角三角形的面积等于两条直角边的乘积的一半;直角三角形的斜边上的高等于两条直角边的乘积除以斜边.

练习册系列答案
相关题目
14.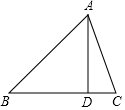 如图,在△ABC中,AC=10,DC=6,AD=8,BC=21,则AB的长为( )
如图,在△ABC中,AC=10,DC=6,AD=8,BC=21,则AB的长为( )
 如图,在△ABC中,AC=10,DC=6,AD=8,BC=21,则AB的长为( )
如图,在△ABC中,AC=10,DC=6,AD=8,BC=21,则AB的长为( )| A. | 15 | B. | 16 | C. | 14 | D. | 17 |
18.为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,10,7,8;
乙:9,5,10,9,7.
(1)将下表填写完整;
(2)若你是教练,根据以上信息,你会选择谁参加设计比赛,理由是什么?
甲:8,7,10,7,8;
乙:9,5,10,9,7.
(1)将下表填写完整;
| 平 均 数 | 方 差 | |
| 甲 | 8 | 1.2 |
| 乙 | 8 | 3.2 |
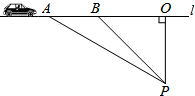 如图,已知测速站P到公路l的距离为40米,一辆汽车在公路l上行驶,测得从点A行驶到点B所用的时间为5秒,并测得∠APO=α,∠BPO=β,计算此车从A到B的平均速度为多少?(已知tanα=$\frac{12}{5}$,sinβ=$\frac{3}{5}$)
如图,已知测速站P到公路l的距离为40米,一辆汽车在公路l上行驶,测得从点A行驶到点B所用的时间为5秒,并测得∠APO=α,∠BPO=β,计算此车从A到B的平均速度为多少?(已知tanα=$\frac{12}{5}$,sinβ=$\frac{3}{5}$) 如图,在△ABC中,∠ABC=∠ACB,∠A=40°,P是△ABC内一点,且∠1=∠2,求∠BPC的度数.
如图,在△ABC中,∠ABC=∠ACB,∠A=40°,P是△ABC内一点,且∠1=∠2,求∠BPC的度数. 如图,已知∠B=43°,∠BDC=43°,∠A=∠1,试说明∠2=∠BDE.
如图,已知∠B=43°,∠BDC=43°,∠A=∠1,试说明∠2=∠BDE.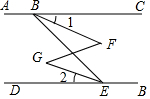
 通州广场上有一旗杆,你能用一些简易的工具,根据全等三角形的有关知识,测出旗杆的高吗?画出示意图,并作说明.
通州广场上有一旗杆,你能用一些简易的工具,根据全等三角形的有关知识,测出旗杆的高吗?画出示意图,并作说明.