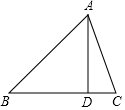如图.在△ABC中.AC=10.DC=6.AD=8.BC=21.则AB的长为( )A．15B．16C．14D．17 题目和参考答案——青夏教育精英家教网—

题目内容

14．

如图，在△ABC中，AC=10，DC=6，AD=8，BC=21，则AB的长为（　　）

A．

B．

C．

D．

分析先根据勾股定理的逆定理判断出△ADC的形状，再由勾股定理即可得出结论．

解答解：∵AC=10，DC=6，AD=8，6²+8²=10²，
∴△ADC是直角三角形，
∴AD⊥BC，
∴∠ADB=90°．
在Rt△ABD中，
∵AD=8，BD=BC-DC=21-6=15，
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{{8}^{2}+1{5}^{2}}$=17．
故选D．

点评本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．

练习册系列答案

学段衔接提升方案赢在高考寒假作业系列答案

新校园快乐假期系列寒假生活指导系列答案

新思维寒假作业系列答案

相关题目

4．配方：x²-6x+9=（x-3）²．

5．（1）用数轴上的点表示下列各数：
-5，2.5，3，-$\frac{5}{2}$，0，-|-3|，3$\frac{1}{2}$．

（2）用“＜”号把各数从小到大连起来．

2．某企业年产值9850 000万元，把9850 000这个数用科学记数法表示为9.85×10⁶．

19．

M为正方形ABCD内一点，MB=2，按逆时针方向旋转△BMC到△BM′A，求MM′的长．

6．

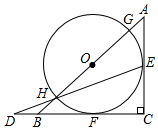如图，△ABC是等腰直角三角形，AC=BC=2a，以斜边AB上的点O为圆心的圆分别与AC，BC相切于点E，F，与AB分别交于点G，H，且EH的延长线和CB的延长线交于点D，则CD的长为（1+$\sqrt{2}$）a．

3．已知x与y之间满足一次函数关系，部分对应值如下表所示，则y关于x的一次函数表达式为y=-$\frac{1}{5}$x+50．

x	50	60	90	120
y	40	38	32	26

6．

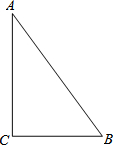在直角三角形ABC中，∠C=90°，AB=5，BC=3．求斜边上的高线及中线的长．

试题分类