题目内容
9. 如图,兴修水利开渠,其断面为等腰梯形,要与水平线的夹角为60°,湿透周长为定制l米(l=AB+BC+CD),问渠深x为$\frac{\sqrt{3}}{4}$l米时,可使水流量最大?
如图,兴修水利开渠,其断面为等腰梯形,要与水平线的夹角为60°,湿透周长为定制l米(l=AB+BC+CD),问渠深x为$\frac{\sqrt{3}}{4}$l米时,可使水流量最大?
分析 设横截面面积为S,由条件知要使流量最大,只要求横截面积最大即可,作AE⊥BC,则AE=DF=x,利用三角函数求得AB=CD=$\frac{AE}{sin60°}$=$\frac{2\sqrt{3}}{3}$x、BE=$\frac{AE}{tan60°}$=$\frac{\sqrt{3}}{3}$x,根据l=AB+BC+CD得BC=l-(AB+CD)=l-$\frac{4\sqrt{3}}{3}$x,AD=BC+2BE=l-$\frac{4\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$x=1-$\frac{2\sqrt{3}}{3}$x,根据梯形面积公式求得S=$\frac{1}{2}$(1-$\frac{2\sqrt{3}}{3}$x+l-$\frac{4\sqrt{3}}{3}$x)•x=-$\frac{2\sqrt{3}}{3}$x2+lx,由二次函数的性质得出其最值情况可得答案.
解答 解:设横截面面积为S,由条件知要使流量最大,只要求横截面积最大即可.
过点A作AE⊥BC于点E,作DF⊥BC于点F,
则AE=DF=x,
则AB=CD=$\frac{AE}{sin60°}$=$\frac{2\sqrt{3}}{3}$x,BE=$\frac{AE}{tan60°}$=$\frac{\sqrt{3}}{3}$x,
∵湿透周长为定制l米(l=AB+BC+CD),
∴BC=l-(AB+CD)=l-$\frac{4\sqrt{3}}{3}$x,AD=BC+2BE=l-$\frac{4\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$x=1-$\frac{2\sqrt{3}}{3}$x,
∴S=$\frac{1}{2}$(1-$\frac{2\sqrt{3}}{3}$x+l-$\frac{4\sqrt{3}}{3}$x)•x=-$\frac{2\sqrt{3}}{3}$x2+lx,
则当x=-$\frac{l}{2×(-\frac{2\sqrt{3}}{3})}$=$\frac{\sqrt{3}}{4}$l时,S取得最大值,
故答案为:$\frac{\sqrt{3}}{4}$l.
点评 本题主要考查二次函数的应用,根据题意明确要使流量最大,只要求横截面积最大是解题的根本,由题中数据表示出梯形的上下底的长是解题的关键.

 灵星计算小达人系列答案
灵星计算小达人系列答案自2014年12月28日北京公交地铁调价以来,人们的出行成本发生了较大的变化. 小林根据新闻,将地铁和公交车的票价绘制成了如下两个表格。(说明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他类似)
|
|
根据以上信息回答下列问题:
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣。
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费________元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交________元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?
| A. | (x+2y)(x-2y)=x2-4y2 | B. | x2y-xy2-1=xy(x-y)-1 | ||
| C. | a2-4ab+4b2=(a-2b)2 | D. | 2a2-2a=2a2(1-$\frac{1}{a}$) |


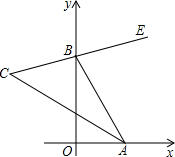 如图,在平面直角坐标系中,点A与点B分别在x轴与y轴的正半轴上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠C的大小是否随点A、B的移动而发生变化?如果保持不变,求出∠C的大小;如果随点A、B的移动而发生变化,请求出变化范围.
如图,在平面直角坐标系中,点A与点B分别在x轴与y轴的正半轴上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠C的大小是否随点A、B的移动而发生变化?如果保持不变,求出∠C的大小;如果随点A、B的移动而发生变化,请求出变化范围. 如图,⊙O是四边形ABCD的内切圆,切点为E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四边形ABCD的周长.
如图,⊙O是四边形ABCD的内切圆,切点为E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四边形ABCD的周长. 如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别切于L、M、N、P,且AB=10cm,CD=5cm,则四边形ABCD周长为30cm.
如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别切于L、M、N、P,且AB=10cm,CD=5cm,则四边形ABCD周长为30cm. 某公用电话亭打电话时,需付电话费y(元)与通话时间x(min)之间的函数关系式用图象表示为直线,小文打了8分钟付费2.2元.
某公用电话亭打电话时,需付电话费y(元)与通话时间x(min)之间的函数关系式用图象表示为直线,小文打了8分钟付费2.2元.