题目内容
14.结合具体的数的运算,归纳有关特例,然后比较下列代数式的大小.(1)已知 0<a<1,则比较$\frac{1}{a}$<$\frac{1}{{a}^{2}}$(填>,=,<)
(2)如果a<0,给出:a=-$\frac{1}{2}$,a=-0.25,a=-2,a=-5,利用给出的a的值,通过数的运算,归纳有关特例,说明a与$\frac{1}{a}$ 的大小关系.
分析 (1)0<a<1,判断出a与a2的大小关系,即可推得$\frac{1}{a}$、$\frac{1}{{a}^{2}}$的大小关系.
(2)如果a<0,将给定的数值带入确定若干组a和$\frac{1}{a}$的值,归纳出a与$\frac{1}{a}$ 的大小关系即可.
解答 解:(1)0<a<1,a>a2,
∴$\frac{1}{a}$<$\frac{1}{{a}^{2}}$;
例如a=0.5时,a2=0.25,
$\frac{1}{a}$=$\frac{1}{0.5}$=2,$\frac{1}{{a}^{2}}$=$\frac{1}{0.25}$=4,
∴$\frac{1}{a}$<$\frac{1}{{a}^{2}}$.
(2)a=-$\frac{1}{2}$时,$\frac{1}{a}$=-2,
-$\frac{1}{2}$>-2;
a=-0.25时,$\frac{1}{a}$=-4,
-0.25>-4;
a=-2时,$\frac{1}{a}$=-0.5,
-2<-0.5;
a=-5时,$\frac{1}{a}$=-0.2,
-5<-0.2;
当-1<a<0时,a>$\frac{1}{a}$;
当a<-1时,a<$\frac{1}{a}$;
当a=-1时,a=$\frac{1}{a}$.
故答案为:<.
点评 此题主要考查了有理数大小比较的方法,考查了分类讨论思想的应用,要熟练掌握.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
6. 如图,一根直尺EF压在三角形30°的角∠BAC上,与两边AC、AB交于M、N,那么∠CME+∠BNF是( )
如图,一根直尺EF压在三角形30°的角∠BAC上,与两边AC、AB交于M、N,那么∠CME+∠BNF是( )
 如图,一根直尺EF压在三角形30°的角∠BAC上,与两边AC、AB交于M、N,那么∠CME+∠BNF是( )
如图,一根直尺EF压在三角形30°的角∠BAC上,与两边AC、AB交于M、N,那么∠CME+∠BNF是( )| A. | 135° | B. | 150° | C. | 180° | D. | 不能确定 |
19. 如图,ABCD是⊙O内接矩形,半径r=2,AB=2,E,F分别是AC,CD上的动点,且AE=CF,则BE+BF的最小值是( )
如图,ABCD是⊙O内接矩形,半径r=2,AB=2,E,F分别是AC,CD上的动点,且AE=CF,则BE+BF的最小值是( )
 如图,ABCD是⊙O内接矩形,半径r=2,AB=2,E,F分别是AC,CD上的动点,且AE=CF,则BE+BF的最小值是( )
如图,ABCD是⊙O内接矩形,半径r=2,AB=2,E,F分别是AC,CD上的动点,且AE=CF,则BE+BF的最小值是( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{7}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
6.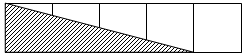 如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )
如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )
 如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )
如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
1.下列各式中,正确的是( )
| A. | $\frac{1+b}{a+2b}$=$\frac{1}{a+2}$ | B. | $\frac{a-2}{{a}^{2}-4}$=$\frac{1}{a-2}$ | ||
| C. | $\frac{a+2}{a-2}$=$\frac{{a}^{2}-4}{(a-2)^{2}}$ | D. | $\frac{-1-b}{a}$=-$\frac{1-b}{a}$ |
 )]
)] 如图,四个半径均为3cm的等圆依次外切,且∠O=90°,则图中阴影部分的面积为36cm2.
如图,四个半径均为3cm的等圆依次外切,且∠O=90°,则图中阴影部分的面积为36cm2. 如图,兴修水利开渠,其断面为等腰梯形,要与水平线的夹角为60°,湿透周长为定制l米(l=AB+BC+CD),问渠深x为$\frac{\sqrt{3}}{4}$l米时,可使水流量最大?
如图,兴修水利开渠,其断面为等腰梯形,要与水平线的夹角为60°,湿透周长为定制l米(l=AB+BC+CD),问渠深x为$\frac{\sqrt{3}}{4}$l米时,可使水流量最大?