题目内容
4. 如图,⊙O是四边形ABCD的内切圆,切点为E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四边形ABCD的周长.
如图,⊙O是四边形ABCD的内切圆,切点为E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四边形ABCD的周长.
分析 首先证明AB+CD=BC+AD,再证明∠DOC=90°,理由勾股定理求出CD,即可解决问题.
解答 解:如图,
∵⊙O是四边形ABCD的内切圆,切点为E,F,G,H,
∴AF=AG,BH=BG,CH=CE,DE=DF,
∴BH+CH+AF+DF=BG+CE+AG+DE,
即BC+AD=AB+CD,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵∠ODE=$\frac{1}{2}$∠ADC,∠OCD=$\frac{1}{2}$∠DCB,
∴∠ODC+∠OCD=90°,
∴∠DOC=90°,
在Rt△DOC中,CD=$\sqrt{O{D}^{2}+O{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵AB=CD=10,
∴AB+CD=BC+AD=20,
∴四边形ABCD的周长为20.
点评 此题主要考查了切线长定理、平行线的性质、直角三角形的判定、勾股定理等知识,正确利用切线长定理得出相等的线段是解题关键,记住本题的结论:圆的外切四边形对边和相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.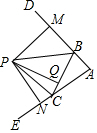 如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )
如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )
 如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )
如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )| A. | PM>PN>PQ | B. | PM<PN<PQ | C. | PM=PN=PQ | D. | PM=PN>PQ |
13. 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )
 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )| A. | 一直不变 | B. | 一直减小 | C. | 一直增大 | D. | 先减小后增大 |
11.下列运算正确的是( )
| A. | $\sqrt{8}$÷$\sqrt{2}$=2 | B. | 5$\sqrt{3}$•5$\sqrt{2}$=5$\sqrt{6}$ | C. | 2$\sqrt{3}$+3$\sqrt{2}$=5$\sqrt{6}$ | D. | $\sqrt{(-6)^{2}}$=-6 |
 的绝对值是( )
的绝对值是( ) B. -
B. - C. 2 D. -2
C. 2 D. -2 将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m,n)表示第m排的第n个数,如(4,2)表示的数是 $\sqrt{6}$,则(5,4)与(18,15)表示的两数之积是2$\sqrt{3}$.
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m,n)表示第m排的第n个数,如(4,2)表示的数是 $\sqrt{6}$,则(5,4)与(18,15)表示的两数之积是2$\sqrt{3}$. 如图,兴修水利开渠,其断面为等腰梯形,要与水平线的夹角为60°,湿透周长为定制l米(l=AB+BC+CD),问渠深x为$\frac{\sqrt{3}}{4}$l米时,可使水流量最大?
如图,兴修水利开渠,其断面为等腰梯形,要与水平线的夹角为60°,湿透周长为定制l米(l=AB+BC+CD),问渠深x为$\frac{\sqrt{3}}{4}$l米时,可使水流量最大?