题目内容
18. 某公用电话亭打电话时,需付电话费y(元)与通话时间x(min)之间的函数关系式用图象表示为直线,小文打了8分钟付费2.2元.
某公用电话亭打电话时,需付电话费y(元)与通话时间x(min)之间的函数关系式用图象表示为直线,小文打了8分钟付费2.2元.
分析 设当x≥3时,需付电话费y(元)与通话时间x(min)之间的函数关系式为y=kx+b(k≠0),根据图形找出点的坐标利用待定系数法即可求出y关于x的函数关系式,再代入x=8即可得出结论.
解答 解:设当x≥3时,需付电话费y(元)与通话时间x(min)之间的函数关系式为y=kx+b(k≠0),
将点(3,0.7)、(4,1)代入y=kx+b中,
$\left\{\begin{array}{l}{3k+b=0.7}\\{4k+b=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=0.3}\\{b=-0.2}\end{array}\right.$,
∴需付电话费y(元)与通话时间x(min)之间的函数关系式为y=0.3x-0.2(x≥3).
当x=8时,y=0.3x-0.2=0.3×8-0.2=2.2.
故答案为:2.2.
点评 本题考查了一次函数的应用以及利用待定系数法求出一次函数解析式,观察函数图象找出点的坐标,利用待定系数法求出函数关系式是解题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
6.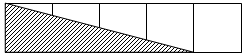 如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )
如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )
 如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )
如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
13. 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )
 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )| A. | 一直不变 | B. | 一直减小 | C. | 一直增大 | D. | 先减小后增大 |
4.下列说法正确的是( )
①0是整数
②0是正数
③数轴上原点两侧的数互为相反数
④整数和分数统称为有理数.
①0是整数
②0是正数
③数轴上原点两侧的数互为相反数
④整数和分数统称为有理数.
| A. | ①② | B. | ①③ | C. | ①④ | D. | ①②③④ |
5.计算:3+(-2)结果正确的是( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |

 如图,兴修水利开渠,其断面为等腰梯形,要与水平线的夹角为60°,湿透周长为定制l米(l=AB+BC+CD),问渠深x为$\frac{\sqrt{3}}{4}$l米时,可使水流量最大?
如图,兴修水利开渠,其断面为等腰梯形,要与水平线的夹角为60°,湿透周长为定制l米(l=AB+BC+CD),问渠深x为$\frac{\sqrt{3}}{4}$l米时,可使水流量最大?