题目内容
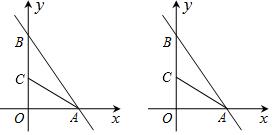
1. 如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别切于L、M、N、P,且AB=10cm,CD=5cm,则四边形ABCD周长为30cm.
如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别切于L、M、N、P,且AB=10cm,CD=5cm,则四边形ABCD周长为30cm.
分析 理由切线长定理,首先证明AB+CD=AD+BC,由此即可解决问题.
解答 解:∵四边形ABCD的边AB、BC、CD、DA和⊙O分别切于L、M、N、P,
∴AP=AL,BM=BL,CM=CN,DN=DP,
∴AL+BL+DN+CN=AP+BM+DP+CM,
即AB+CD=AD+BC,
∵AB=10cm,CD=5cm,
∴AB+CD=AD+BC=15cm,
∴四边形ABCD的周长为30cm.
故答案为30.
点评 此题主要考查了切线长定理,正确利用切线长定理得出相等的线段是解题关键,记住本题的结论:圆的外切四边形对边和相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.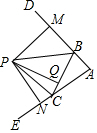 如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )
如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )
 如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )
如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )| A. | PM>PN>PQ | B. | PM<PN<PQ | C. | PM=PN=PQ | D. | PM=PN>PQ |
6.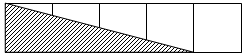 如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )
如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )
 如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )
如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
 n=mn-n,例如3
n=mn-n,例如3 5=3×5-5=10,则(-6)
5=3×5-5=10,则(-6)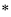 4=________。
4=________。 如图,兴修水利开渠,其断面为等腰梯形,要与水平线的夹角为60°,湿透周长为定制l米(l=AB+BC+CD),问渠深x为$\frac{\sqrt{3}}{4}$l米时,可使水流量最大?
如图,兴修水利开渠,其断面为等腰梯形,要与水平线的夹角为60°,湿透周长为定制l米(l=AB+BC+CD),问渠深x为$\frac{\sqrt{3}}{4}$l米时,可使水流量最大?
 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )